
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 2, 2019
Se presenta el desarrollo de un Brazo Robótico para Cirugía Laparoscópica (BRCL) mediante cinemática directa, por los métodos de matriz de transformación homogénea y los cuaternios es posible resolver el problema de la cinemática directa del BRCL, el cual puede ser utilizado por médicos cirujanos, quienes manipularan a través de cinco botones el desplazamiento de la trayectoria del robot.
Palabras clave: Brazo robótico, cirugía laparoscópica, cinemática directa
We present the development of a Robotic Arm for Laparoscopic Surgery (RALS) through direct kinematics, by the methods of homogenous transformation matrix and the quaternios it is possible to solve the problem of the direct kinematics of the RALS, which can be used by surgeons, who will manipulate the displacement of the robot's trajectory through five buttons.
Key words: Arm robotic, direct kinematic, laparoscopic surgery
La cirugía laparoscópica es la técnica que permite la mejor visibilidad de los órganos internos del ser humano, por ejemplo: intestinos, estómago, vesícula biliar, órganos pélvicos, etc.
La cirugía laparoscópica constituye un avance en el siglo XX, puesto que permite realizar cirugías en las cavidades orgánicas evitando grandes incisiones y por ende es mínimamente invasiva.
Esta técnica ha revolucionado completamente el mundo de la cirugía moderna. A pesar de sus ventajas se presentan diversas dificultades para el cirujano, siendo las más destacables la pérdida de: la sensación de profundidad-táctil, fuerza, destreza manual y coordinación natural de ojos-manos, habilidades apticas. La principal motivación para el desarrollo de los robots quirúrgicos es la posibilidad de eliminar errores. Los robots han permitido mejorar la capacidad quirúrgica de los cirujanos.
La cirugía robótica brinda ventajas que facilitan la operación y la realización de procedimientos quirúrgicos, en técnicas mínimamente invasivas.
“La Sociedad Americana de Cirugía Gastrointestinal y Endoscópica (Society of American Gastrointestinal and Endoscopic Surgeons, SAGES) define la cirugía robótica como un procedimiento quirúrgico realizado con tecnología que facilita la interacción entre el cirujano y el paciente”.
En el estudio de la cinemática de robots aborda el problema geométrico del movimiento de sistemas mecánicos sin tomar en cuenta las fuerzas que lo producen, el cual se centra en el análisis y diseño del desplazamiento de la trayectoria del robot.
En la estructura mecánica del robot se considera el tipo de articulaciones (lineal o rotacional), para la clasificación general de robots manipuladores industriales, también conocidos como brazos robots: antropomórfico, esférico, cilíndrico, SCARA y cartesiano.
En un espacio tridimensional el posicionamiento del robot requiere de seis coordenadas: tres para el posicionamiento y tres para la orientación. La relación que existe entre las coordenadas articulares con las coordenadas cartesianas y su orientación se conoce como cinemática directa. La cinemática inversa se describe como la relación entre las coordenadas articulares en función de las coordenadas cartesianas y ángulos de orientación.
La metodología de Denavit -Hartenberg permite obtener la posición y orientación, de tal manera que establece la estructura matemática de las transformaciones homogéneas.
Los cuarteniones definidos por Hamilton, como matrices de rotación, pueden ser utilizados para trabajar giros y orientación, puesto que la matriz de transformación homogénea y los cuaternios son métodos alternativos, de esta manera es posible resolver la cinemática directa del robot.
En este trabajo se desarrolló un robot industrial tipo SCARA para el BCRL.
La cinemática describe y analiza el efecto del movimiento sobre los cuerpos sin tener en cuenta las causas. En este proyecto, lo importante es analizar los aspectos geométricos y coordenadas de movimiento descrito por la posición del cuerpo.
Existen dos problemas fundamentales para resolver la cinemática del robot.
La cinemática directa se refiere a la utilización de las ecuaciones cinemáticas de un robot para determinar la posición deseada del efector final, es decir, especificar los movimientos de un robot de tal manera realice las tareas deseadas.
Por consiguiente, consiste en obtener la posición en el espacio de la estructura a partir de los valores de las coordenadas, las cuales están asociadas a las articulaciones y definen las propiedades de movimiento, por lo tanto, la variable de las articulaciones de revolución generalizada, será un ángulo, y para las prismáticas un desplazamiento.
Uno de los métodos más utilizados es el de Denavit-Hartenberg y la fórmula de producto de exponenciales.
Denavit y Hartenberg [1955] propusieron un método sistemático y generalizado de utilizar álgebra matricial para describir y representar la geometría espacial de los elementos de un brazo con respecto a un sistema de referencia fijo.
Dicho método hace uso de la matriz de transformación homogénea el cual describe la relación espacial entre dos elementos rígidos adyacentes así reduciendo el problema cinemático al hallar una matriz de transformación 4 x 4 que relacione la localización espacial del extremo del robot.

Los cuaterniones o cuaternios están definidos por Hamilton [HALMITON-69], pueden ser utilizados como herramienta matemática de gran diversidad computacional para trabajar con giros y orientaciones.
Un cuaternio es una combinación lineal de la forma:
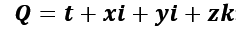
donde t,x,y,z son números reales.
Puesto que las matrices de transformación homogénea y los cuaternios son métodos alternativos para representar transformaciones de rotación y desplazamiento, en el cual será posible utilizar estos dos procedimientos de manera equivalente para la resolución del problema cinemático directo.
En la figura 1, se muestra la morfología del BRCL, el cual consta de cuatro eslabones y además un efector final, tres articulaciones rotacionales y una prismática.
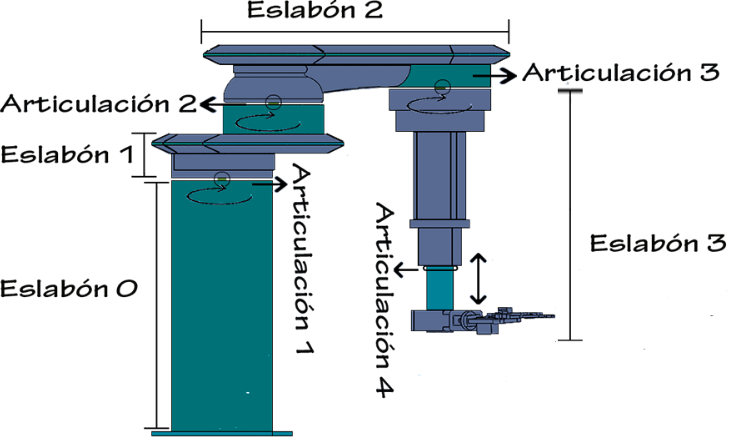
Figura 1. Morfología del BRCL
De acuerdo con la teoría ya descrita, los cálculos se resuelven por medio de MATLAB.
Para la configuración BRCL se producen el siguiente conjunto de parámetros Denavit-Hartenberg que se muestran en la tabla 1.
Tabla 1. Parámetros DH del BRCL
| Eslabón | li | αi | di | θi |
|---|---|---|---|---|
| 1 | l2 | 0 | β1 | q1 |
| 2 | l2 | 0 | β2 | q2 |
| 3 | l3 | 0 | β3 | q3 |
| 4 | l4 | π | d4 | 0 |
El indicador li se define como la distancia a lo largo del eje xi, desde el origen del sistema de referencia coordenado i-1 hasta la intersección del eje zi-1 con el eje xi.
El siguiente parámetro es el ángulo (se denota αi) entre los ejes zi y zi-1, su medición es respecto a un plano normal a xi. Una medición de ángulo positivo para αi se toma en dirección del eje zi-1 hacia zi.
La función de cinemática directa del BRCL se define como:
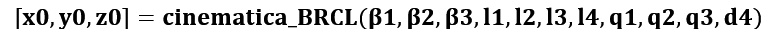
donde los argumentos de entrada son los parámetros geométricos: β1,β2,β3,l1,l2,l3,l4 y las variables articulares q1,q2,q3,d4, como se ilustra en la figura 2. Esta función retorna las coordenadas x0, y0, z0 en el espacio cartesiano del sistema de referencia fijo Σ0(x0, y0, z0).
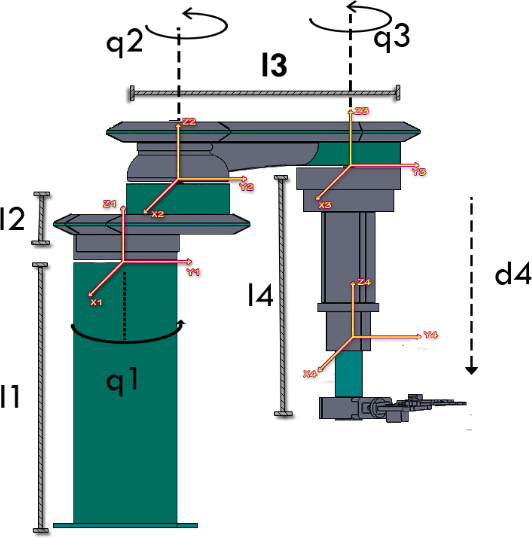
Figura 2. Parámetros geométricos
En la figura 3 se muestra la implementación del sistema de manejo, cada botón representa un movimiento para el funcionamiento del BRCL, los comandos a utilizar son: sujetar, arriba, abajo, izquierda y derecha. La botonera va conectada a una Raspberry PI para poder enviar las señales de movimiento al BRCL.
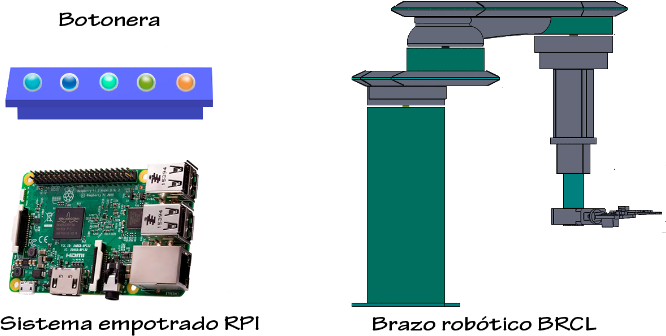
Figura 3. Sistema de conexión
El prototipo se diseñó mediante herramientas CAD, se aplicaron conocimientos de física, matemáticas, electrónica y programación.
Este tipo de prototipo generan nuevas soluciones a los problemas de salud, resultado de la interacción entre la investigación científica y la ciencia aplicada.