Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud
Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 2, 2019
En este trabajo se quiere conocer el comportamiento del flujo de campo magnético que se utiliza en tratamiento clínicos con radiofrecuencia y sus rangos de aplicación.
Los estudios científicos sobre la impedancia bioeléctrica muestran que se necesita 1MHz para penetrar en una célula del cuerpo, cuanto mayor sea la frecuencia menor será la resistencia. Tomando en cuenta que se debe aplicar una determinada frecuencia para hacer vibrar una determinada célula.
Al medir el campo magnético de las antenas de radio frecuencia, se puede calcular la frecuencia a la que están resonando determinadas células y por lo tanto saber si las células de nuestro interés se están excitando.
Palabras claves: Campos magnéticos, radiofrecuencia, tratamiento
In this work we want to know the behavior of the magnetic field flow that is used in the radiofrequency clinical treatment and its application ranges.
Studies on bioelectrical impedance show that 1 MHz is needed to penetrate a body cell, the higher the frequency the lower the resistance. Take into account that a certain frequency must be applied to vibrate a certain cell.
By measuring the magnetic field of RF diseases, it is possible to calculate the frequency while they are exciting certain cells and therefore to know if the cells of our interest are resonating.
Keywords: Magnetic fields, radiofrequency, treatment
Los campos electromagnéticos son usados en medicina como tratamiento en patologías humanas [1]. En la literatura se reporta que usando frecuencias ultrasónica o de radio es posible hacer resonar a átomos o moléculas de tejido humano en determinadas frecuencias El rango total de frecuencias resonantes del cuerpo humano es de 62 a 68 Hz aproximadamente [2] Esta técnica de resonancia sería posible aplicarla para otros átomos que estén presentes en cáncer [3] Se sabe que usando frecuencias resonantes, el cáncer es vulnerable entre las frecuencias de 100000 Hz y 300000 Hz[4].
En la medicina el uso de campos magnéticos se refiere principalmente en la obtención de imágenes por resonancia magnética, en el día a día estamos expuestos a los campos magnéticos, por ejemplo, el campo magnético terrestre y trenes de transporte basados en tecnología de levitación magnética. Sin embargo, la mayor exposición se da en pacientes que son sometidos a estudios médicos, por lo que se ha dedicado gran interés en conocer sus posibles efectos biológicos como parte del concepto de seguridad clínica del paciente [5].
Un campo magnético es un campo vectorial, por lo que tiene dirección y magnitud. La intensidad de un campo magnético (
) puede ser conceptualizada como la cantidad de líneas de campo por unidad de área, estas líneas imaginarias describen la orientación del campo magnético. Matemáticamente la intensidad del campo magnético es descrita en función a la fuerza que este puede ejercer sobre una partícula eléctricamente cargada [6], tal como se muestra en la ecuación 1:
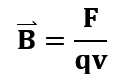
La intensidad de los campos magnéticos constantes no varía en el tiempo, como los utilizados en imagenología por resonancia magnética nuclear que por lo general provienen de imanes con intensidades del rango de 1 T hasta 3 T; una magnitud grande en comparación a la del campo magnético terrestre (aproximadamente 50 μT) [7].
Un siglo antes de que los químicos y los físicos comenzaran a investigar el estado cristalino líquido, los biólogos reconocieron que las células vivas poseían propiedades que ahora llamamos líquido cristalino. Fue durante la “Faraday Society Meeting” en 1933 que surgió la naturaleza cristalina líquida de las estructuras biológicas.
Los científicos han estudiado los tres estados de la materia (gases, líquidos y sólidos) durante dos siglos. Se puede considerar el estado cristalino líquido como el cuarto estado de la materia. La estructura cristalina líquida existe tanto en sistemas animados como inanimados. En los procesos vitales, sus estructuras se encuentran en las membranas celulares y en muchos tejidos corporales.
Los cristales líquidos los encontramos en las pantallas y mediante el envío de electrónica especial se puede cambiar sus propiedades como el color y forma en la pantalla; entonces podríamos mandar vibraciones resonantes y cambiar un cristal líquido biológico; si consideramos que los organismos vivos y las células tienen propiedades de cristales líquidos [8].
Para generar un cambio drástico en la resonancia y por tanto en la vibración de una célula se necesitan, dos frecuencias, un alta y una baja. Y tal como lo hacen los cantantes de ópera, romper un cristal, al ir subiendo el tono de su voz cada vez con una frecuencia más alta.
En ausencia de un campo magnético externo, los vectores de momento magnético de los protones apuntan a cualquier dirección. En presencia de un campo externo los protones adquieren el estado de α o de Β spin. Como el estado α es el de menos energía habrá más población de protones.
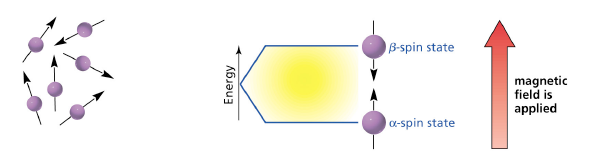
Ilustración 1. (a) Protones sin campo magnético externo aplicado, (b)protones en presencia de un campo magnético externo
Cuando se introduce el campo externo surge una diferencia, mayor, cuanto mayor sea la magnitud del campo. Existe entonces una diferencia de energía entre los estados y el campo externo son directamente proporcionales.
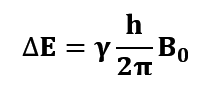
Con h la constante de Planck, B0 la intensidad del campo externo, γ la constante giromagnética en función del momento magnético y ∆E la diferencia de energía entre los estados.
Si un fotón colisiona con la energía adecuada el protón puede pasar del estado α al β. El spin con un sentido paralelo al campo externo puede tomar el contrario.
Un núcleo que se encuentra con el campo magnético y la radiación adecuada, decimos que está en resonancia y toda la energía recibida la utiliza en cambiar de spin. El nombre de Resonancia Magnética Nuclear proviene de ahí. Si tenemos en cuenta las siguientes ecuaciones:
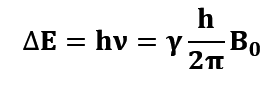
Entonces se observa que la frecuencia ν es directamente proporcional al campo magnético externo B0 y a la constante giromagnética γ
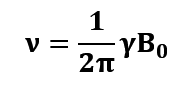
Se realizaron gráficas de mediciones continuas de 10 minutos en cada una de las antenas, obteniendo el valor experimental del campo magnético para posteriormente obtener los valores de las frecuencias a las que se están haciendo resonar los átomos, mediante el uso de la ecuación de la frecuencia, en un principio para el núcleo del átomo de hidrógeno que es el más usado en estudios de resonancia magnética nuclear y algunos núcleos presentes en espectroscopía.
Se estudiaron campos magnéticos que varían entre 0.01mT (425.8 Hz) y 9mT (383220 Hz).
Al tener el valor experimental del campo magnético se puede obtener la frecuencia a la que este campo magnético está haciendo vibrar las moléculas.
Se presentan gráficas del campo magnético y su comportamiento en relación al tiempo, para entender el efecto que tiene, durante la aplicación del tratamiento con un conjunto de antenas de RF, en el isocentro se mantiene constante el campo magnético (véase Ilustración 2).
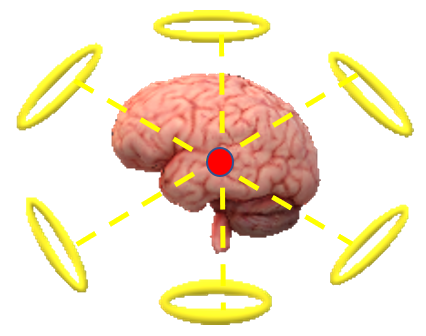
Ilustración 2. Representación de los pulsos de RF dirigidos hacia el isocentro, que en este caso se ilustra como un tumor en el cerebro
Del modelo matemático, se tiene una superposición de campos, con la condición de que en el isocentro no haya variación (promedio aproximado de -0.10148948 mT), y se hacen suposiciones del efecto de resonancia.
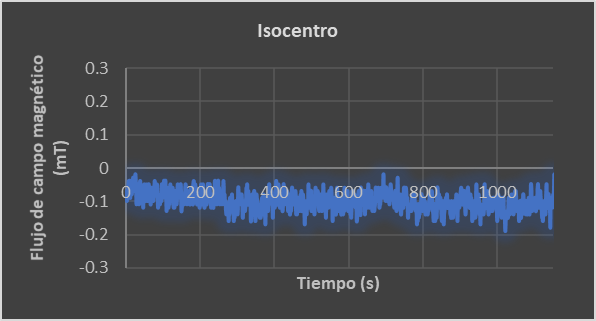
Gráfica 1. Isocentro, en dónde todos los campos se superponen y por lo tanto no existe variación notoria
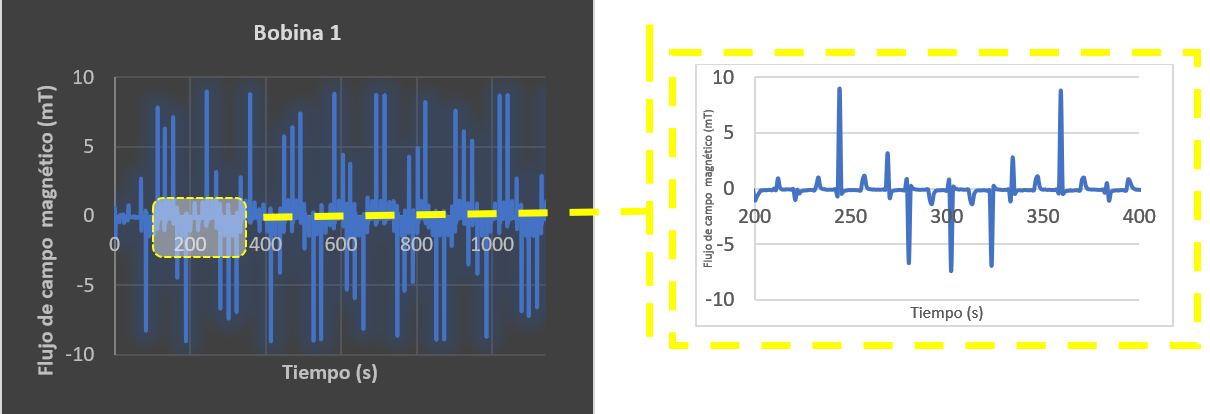
Gráfica 2. bobina 1 y zoom de la gráfica
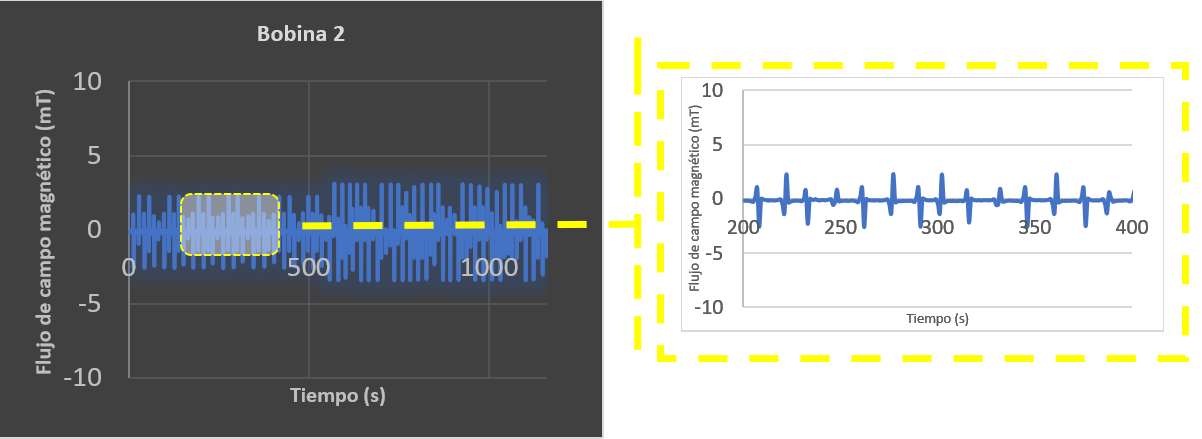
Gráfica 3. Bobina 2 y zoom de la gráfica
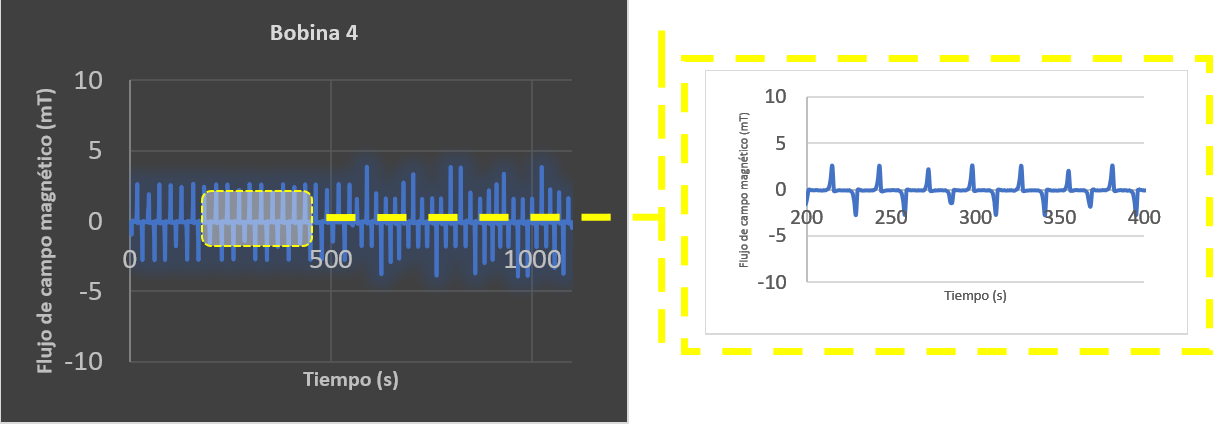
Gráfica 4. Bobina 4 y zoom de la gráfica
De la ecuación (4), tenemos que la frecuencia tiene unidades de Hertz
En la teoría se encuentran valores de γ=γ/2π, por lo tanto, reescribimos la ecuación (4) de la frecuencia
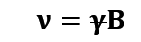
Para el átomo de hidrógeno la constante giromagnética es
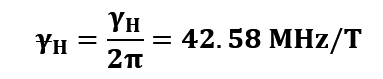
En la tabla 1, se muestran ejemplos de varios núcleos, solamente para los valores extremos de .01 mT, 9 mT y para el valor de -0.101mT el valor en el isocentro.
Tabla 1. Listado de frecuencias para diferentes núcleos usados en espectroscopia.
| Frecuencia | ||||
|---|---|---|---|---|
| núcleo |  [MHz/T] |
Con B=9 mT | B=0.01mT | Con B=-0.101mT |
| 1H | 42.6 | 0.38322 MHz = 383220 Hz | 4.258×10-4 MHz = 425.8 Hz | -4.3026×10-3sup> MHz= -4302.6Hz |
| 2H | 6.53 | 0.05877 MHz = 58770 Hz | 6.53×10-5 MHz = 65.3 Hz | -6.5953×10-4 MHz= -659.53Hz |
| 13C | 10.7 | 0.0963 MHz = 96300 Hz | 1.07×10-4 MHz = 107 Hz | -1.0807×10-3 MHz= -1080.7Hz |
| 19F | 40.1 | 0.3609 MHz = 360900 Hz | 4.258×10-4 MHz = 425.8 Hz | -4.0501×10-3 MHz = -4050.1Hz |
| 23Na | 11.3 | 0.1017 MHz = 101700 Hz | 1.13×10-4 MHz = 113 Hz | -1.1413×10-3 MHz= -1141.3 Hz |
| 31P | 17.2 | 0.1548 MHz = 154800 Hz | 1.72×10-4 MHz = 172 Hz | -1.7372×10-3 MHz= -1737.2Hz |
| 15N | 4.3 | 0.0387 MHz = 38700 Hz | 4.3×10-5MHz = 43 Hz | -4.343×10-4 MHz= -434.3Hz |
| 29Si | 8.465 | 0.07618 MHz = 76180 Hz | 8.465×10-5 MHz= 84.65 Hz | -8.5496×10-4 MHz=-854.965 Hz |
Usando estos datos de las frecuencias, se puede hacer una comparación más factible para los diferentes tipos de canceres. En este caso el Flúor y el Hidrógeno son los núcleos con las frecuencias más altas. Se puede observar que se tienen campos magnéticos del orden de mili teslas; para valores mayores a mili teslas, las frecuencias serán mayores también.
lustración 3. Dona de aproximadamente 81 cm de diámetro
La señal pulsada de salida debe ser de encendido y apagado, ya que las ondas electromagnéticas en organismos vivos y células (si la señal es constante) empieza a inducir calor en ellas y en las células de su alrededor, causando destrucción indiscriminada y lo que se quiere es una destrucción dirigida.
Se necesitan dos frecuencias de entrada, una baja y una alta y la frecuencia más alta debe ser mucho mayor que la frecuencia más pequeña así cuando se llega a la frecuencia más alta entran en resonancia y se empiezan a destruir microorganismos como una copa de cristal. [4]
Se piensa en una dona de diámetro aproximado de 81 cm, en dónde pueda caber una persona y así ser usado para tratamientos en medicina (ver ilustración 3).
La medición de la frecuencia para el átomo de hidrógeno nos da una idea de cómo se puede realizar la misma medición para diferentes átomos y poder obtener las frecuencias de vibración de las proteínas en los tumores cancerígenos
Obtener PDF