
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 4, 2022
El modelo matemático Susceptible- Infectado- Recuperado (SIR), propuesto por el bioquímico escocés William Ogilvy Kermack y el médico militar Anderson Gray McKendrick, describe la dinámica de una epidemia. En este trabajo se muestra el análisis de dos variantes del modelo SIR que considera a la vacunación como un elemento de control. Estos modelos podrían reflejar de manera más precisa los resultados observados en epidemias.
Palabras Claves: Modelo SIR, Vacunación
The Susceptible-Infected-Recovered (SIR) mathematical model, proposed by Scottish biochemist William Ogilvy Kermack and military physician Anderson Gray McKendrick, describes the dynamics of an epidemic. This paper shows the analysis of two variants of the SIR model that considers vaccination as a control element. These models could reflect the results observed in the epidemics more precisely.
Key Words: SIR Model, Vaccination
Un modelo matemático es una representación simplificada por medio de ecuaciones, variables, parámetros, entidades y relaciones entre estos para estudiar el comportamiento de un sistema complejo, sus cambios y situaciones que son difíciles de observar en la vida real [1]. Una enfermedad puede ser observada y analizada a través de modelos matemáticos, los cuales proporcionan información que permite conocer su evolución y generar hipótesis que se puedan probar por medio de simulaciones computacionales utilizando software conocido o mediante la implementación de algoritmos, así como por medio de datos que se obtengan de observaciones y o mediciones. De esta manera, el modelo matemático puede utilizarse para predecir algunos escenarios, sus repercusiones, así como implementar acciones y políticas de salud pública para la prevención y control de propagación de la enfermedad. En particular, el modelo SIR y sus variantes han sido utilizados para el estudio de la pandemia COVID-19 [2], [3], [4], [5], [6].
Modelo SIR
El modelo SIR permite dividir a la población en tres grandes clases [2]. La primera contine a todas las personas susceptibles S, que son todas aquellas que pueden ser contagiadas y no cuentan con inmunidad en contra el virus. La segunda gran clase es la de los infectados I, que son las personas que portan el virus y pueden transmitir la enfermedad. Por último, tenemos la clase de las personas recuperadas R, que tuvieron la enfermedad y que han alcanzado un grado de inmunidad y ya no son capaces de contagiar a la población susceptible. Estas tres clases tiene una interaccionan entre sí, como se muestra en la Figura 1.

Figura 1. El modelo SIR representado esquemáticamente a través de la interacción de tres compartimentos, en los que el flujo es forma concatenada. Más precisamente, la población de susceptibles pasa a la de infectados que a su vez pasa a la de recuperados. No hay interacción directa entre susceptibles y recuperados
De acuerdo con lo que se muestra en la Figura 1, podemos tener las siguientes consideraciones:
De acuerdo con los puntos anteriores se puede construir el modelo SIR, donde N es la población total, S es la población de individuos susceptibles, I es la población de individuos infectados y R es la población de individuos recuperados.
La primera ecuación se describe de la siguiente manera:
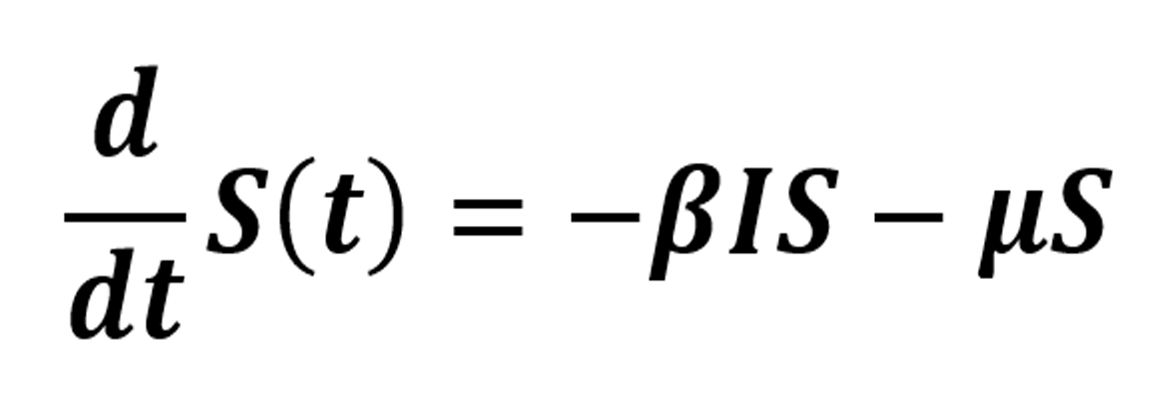
El número de individuos que pasa de la clase de susceptibles a la clase de infectados se encuentra dada por el primer término de la ecuación (1), la cual está determinada por el producto entre la clase de susceptibles, la de infectados y la tasa β. El signo negativo de los dos términos de (1), representa la pérdida de individuos de la población de susceptibles. El término —µS, describe la pérdida de individuos susceptibles que fallecen por muerte natural. La ecuación que describe la dinámica del compartimiento de infectados está dada por
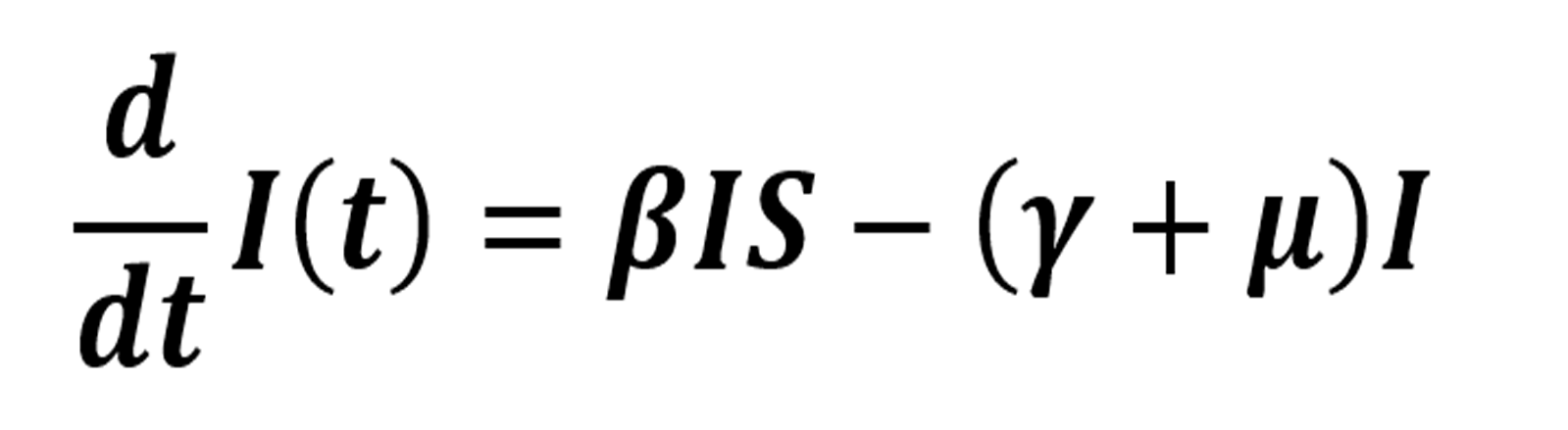
La ecuación (2) muestra el comportamiento de la clase de individuos infectados, la cual está dada por el primer término de (1), es decir, por aquellos individuos que abandonaron el compartimiento de susceptibles porque se contagiaron al estar en contacto con los infectados. En (2), ϒ representa la tasa de individuos infectados que pasan a ser recuperados, por lo que la pérdida de individuos que sale de la clase de infectados a recuperados está dada por ϒI. El término —µI, describe la pérdida de individuos infectados que fallecen por muerte natural. Por último, la ecuación que describe a la clase de población de recuperados es de la forma:
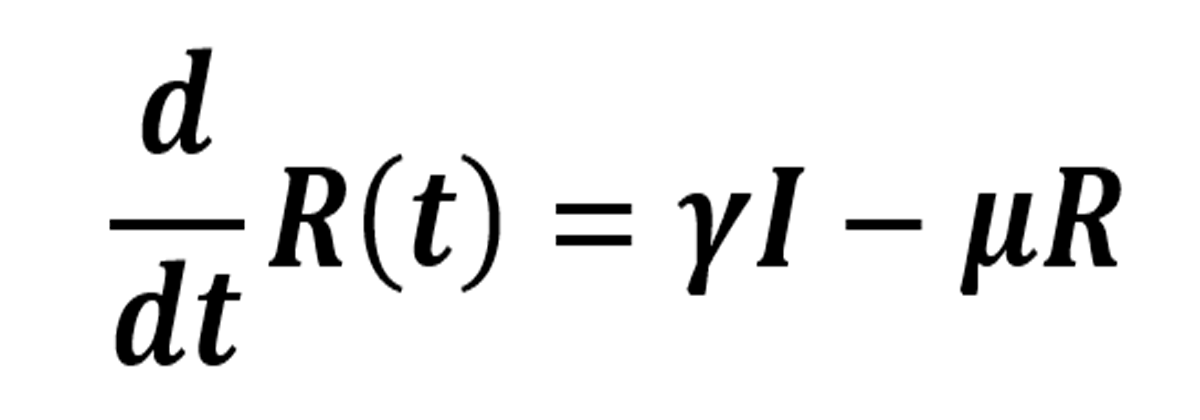
El término -μR, describe la pérdida de individuos recuperados que fallecen por muerte natural.
Debido a que la población total N se divide en S susceptibles, I Infectados y R recuperados, tenemos que N = S + I + R.
De acuerdo con esto, la dinámica de la epidemia puede modelarse por medio del sistema de ecuaciones diferenciales de primer orden dado por las ecuaciones (1) - (3) con las condiciones iniciales S(0) = S0, I(0) = I0, R(0) = R0.
El modelo SIR clásico con vacunación considera que la población de vacunados pasa al compartimiento de los infectados [4], [5]. En este trabajo, vamos a considerar dos variantes.
2.1 Primera Variante
Se considera una variante del modelo SIR tomando a la vacunación como una herramienta de control. En esta variante, se tienen tres clases de poblaciones: La población de Susceptibles S, infectados I y la de protegidos P. Vamos a considerar que la población de protegidos se integra por la población de vacunados y la de recuperados ya que suponemos que cuentan con la misma inmunidad. La interacción que existe entre las clases se puede observar en la Figura 2, donde:
α representa la tasa de individuos vacunados, β es la tasa de individuos que pasa de la clase de susceptibles a la clase de infectados y γ es la tasa de los individuos que pasa de la clase de infectados a la clase de protegidos.
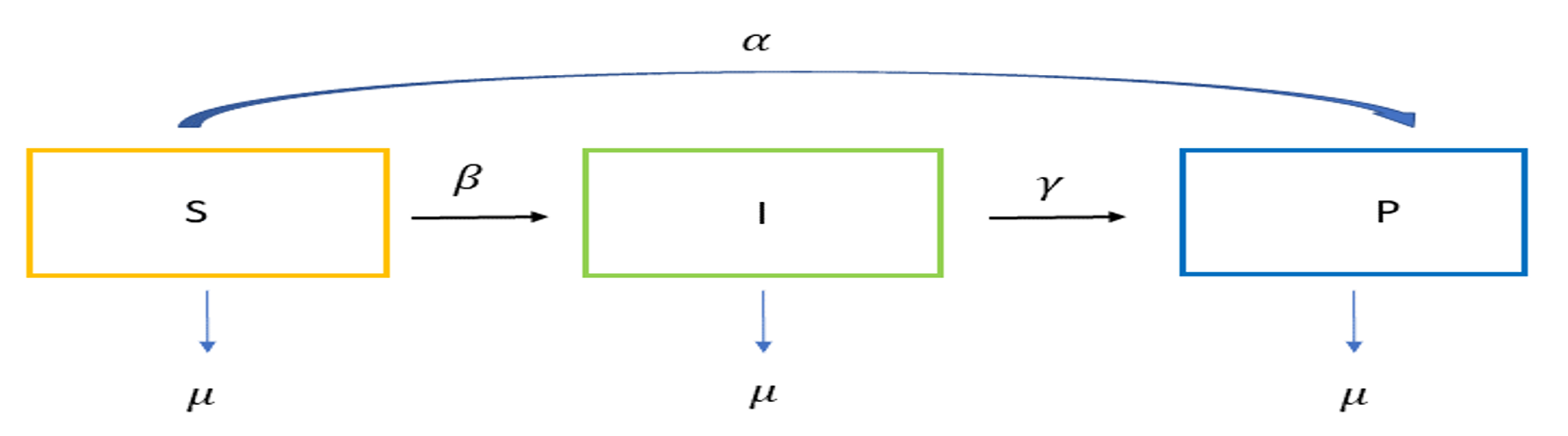
Figura 2. En esta variante del modelo, se considera que la población de vacunados pasa a la de protegidos con una tasa α. Nótese que en esta variante no se considera que los individuos vacunados pasan al compartimiento de los infectados sino directamente al de los protegidos
Con lo anterior podemos determinar el modelo que representa esta variante. En este caso, la variación en la población de individuos susceptibles está determinada por la interacción entre la clase de susceptibles e infectados, así como por la población de susceptibles que han recibido la vacuna. La tasa de individuos vacunados se denota por α. Por simplicidad, en lo que sigue no se considera el término correspondiente a la muerte natural. Así, se tiene la ecuación
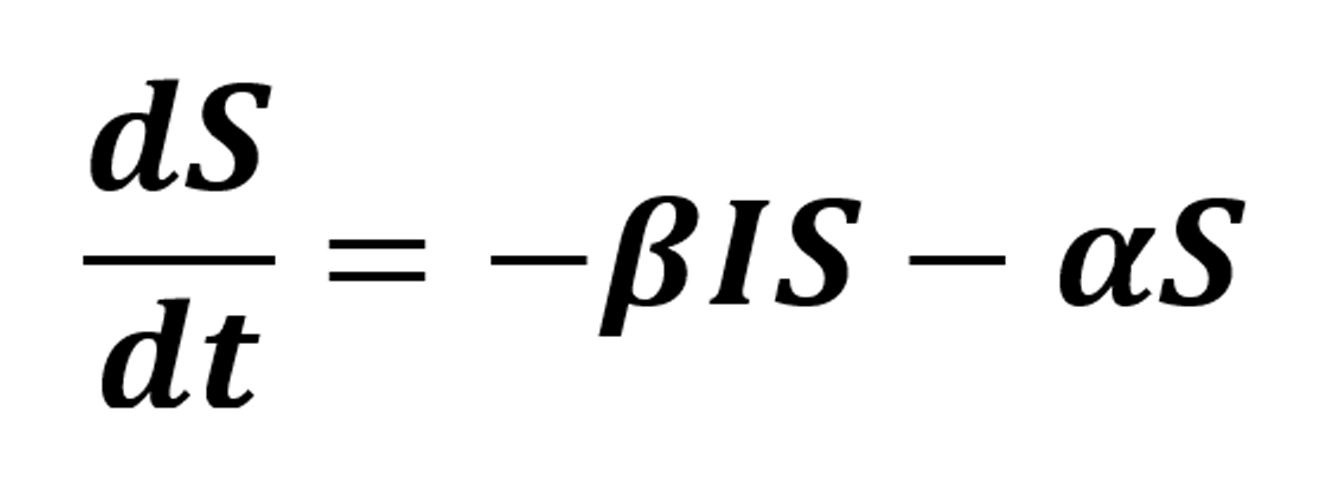
donde el signo negativo en los dos términos representa la pérdida (o salida) de individuos de la clase de susceptibles.
Como en el modelo SIR, el término βSI con signo positivo muestra la ganancia de individuos en la clase de infectados y el término -γI representa a los individuos infectados que se recuperan. En este caso, tenemos la misma ecuación que en el modelo SIR (no estamos considerando la muerte natural):
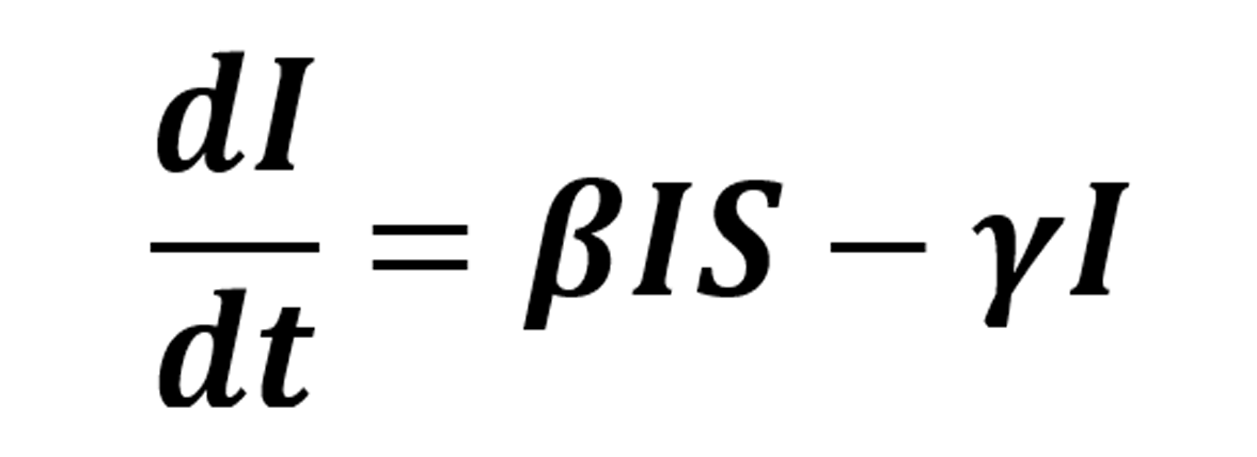
Para la clase de individuos protegidos se consideran los individuos que pasan de la clase de infectados a la de protegidos γI y los individuos que han adquirido inmunidad debido a la vacunación αS:
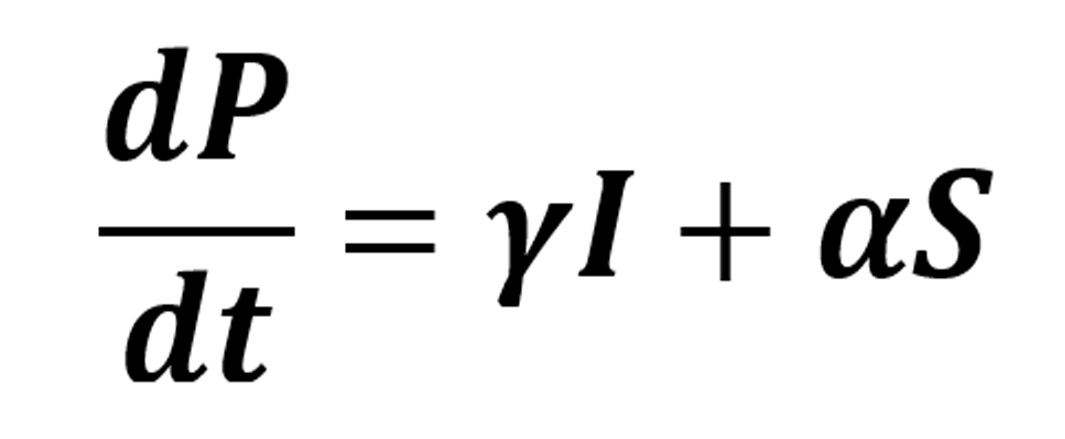
Análogamente al caso del modelo SIR, se tiene que P = N - (S + I). Por ello, la dinámica puede describirse con los compartimientos de susceptibles e infectados, bajo la suposición que la población total N es constante.
El análisis del modelo se realiza a través de los puntos críticos del sistema que son la solución del sistema de ecuaciones algebraicas:
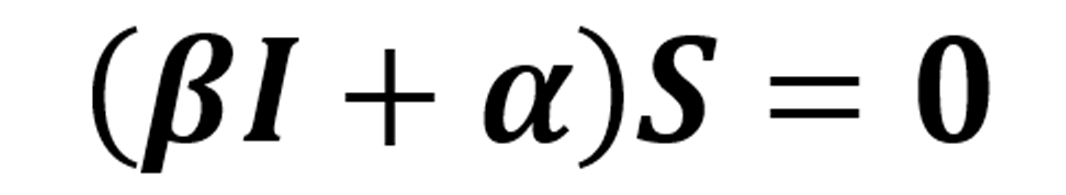
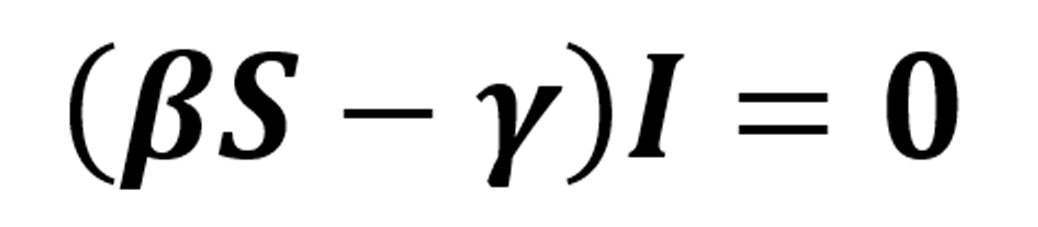
En este caso, están dados por (0, 0) y 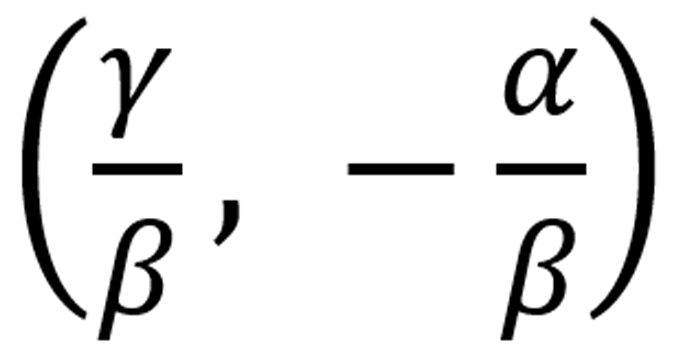 . El punto (0, 0) permite saber que la pandemia se encuentra controlada. Mientras que el punto dado por
. El punto (0, 0) permite saber que la pandemia se encuentra controlada. Mientras que el punto dado por 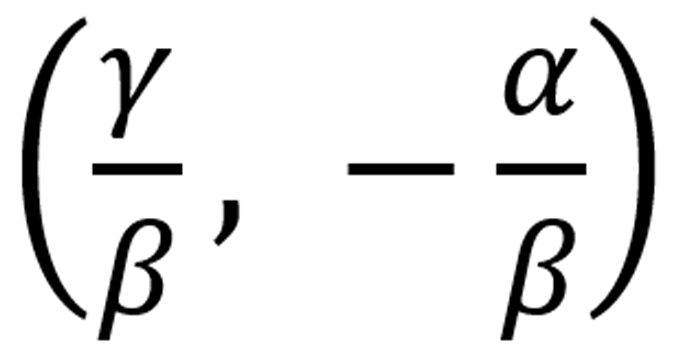 al parecer no tiene interés biológico. Sin embargo, una posible interpretación de este punto es que hay una parte de la población que es inmune o que no infecta (por ello el valor negativo de I.) La matriz jacobiana está dada por:
al parecer no tiene interés biológico. Sin embargo, una posible interpretación de este punto es que hay una parte de la población que es inmune o que no infecta (por ello el valor negativo de I.) La matriz jacobiana está dada por:
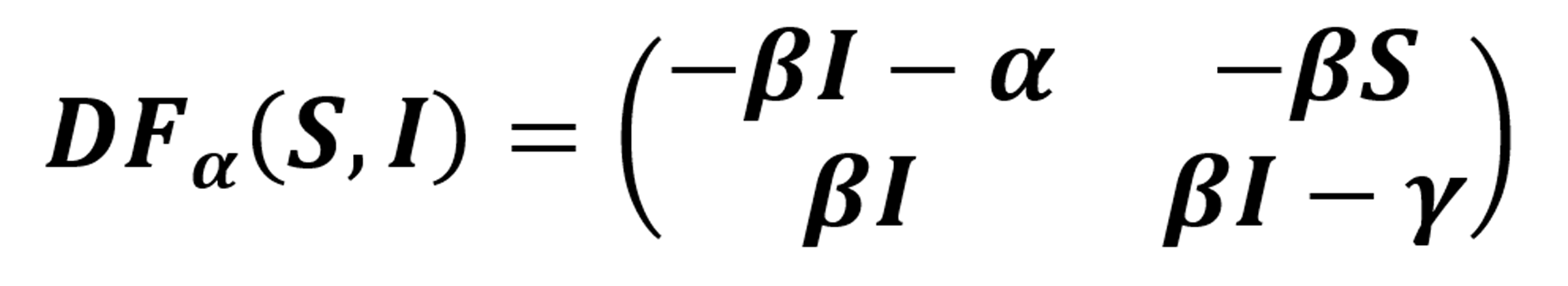
Evaluando (9) en el punto crítico (0, 0), se halla que este punto crítico es un atractor, ya que los valores propios de la matriz son negativos: DFα (0, 0) = 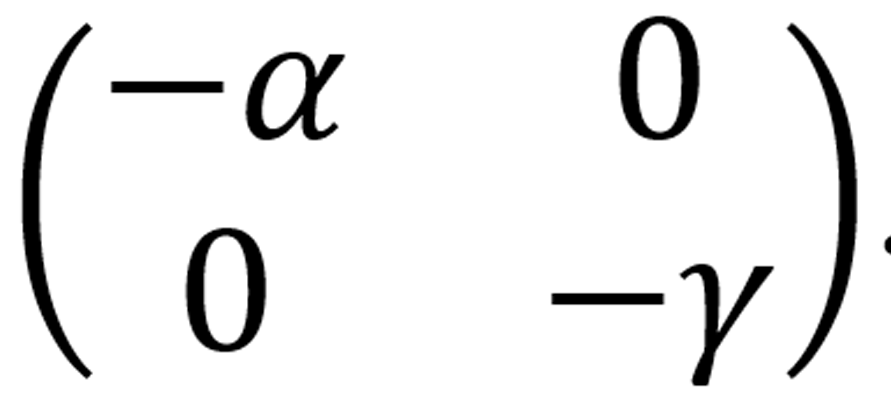 . Esto es congruente con el efecto que se espera de la vacuna.
. Esto es congruente con el efecto que se espera de la vacuna.
2.2 Segunda Variante
Para segunda variante del modelo SIR consideraremos la Figura 3, donde los individuos vacunados se dividirán en dos clases, una de las cuales pasará a la clase de los infectados con una tasa α1 y la otra parte pasará a la clase de los protegidos con una tasa α2.
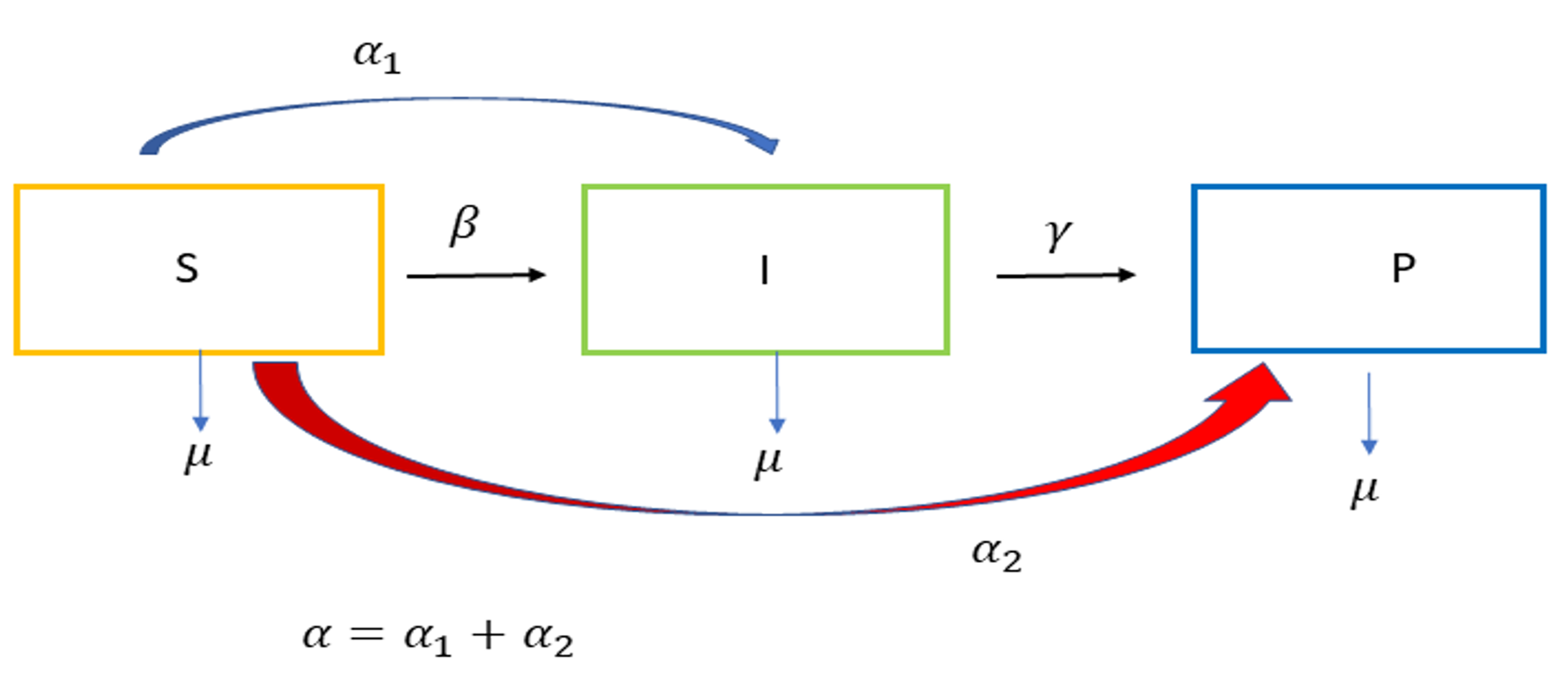
Figura 3. En esta variante del modelo del SIR, se considera que una parte de la población de vacunados pasa a la de protegidos y otra a la de infectados. En este caso, no toda la población susceptible pasa a uno de los compartimientos como en el modelo SIR original y en la primera variante presentada arriba
Para la clase de los susceptibles tenemos la misma ecuación (4) que en la primera variante ya que los individuos abandonan la población susceptible con la misma dinámica. Vamos a considerar que α = α1 + α2, es decir, la tasa de salida de los susceptibles se divide en dos tasas, la que va a los infectados y la otra a la de los protegidos. Como en los modelos anteriores, el término βSI representa la cantidad de individuos que dejan la clase de susceptibles y pasan a la clase de infectados. El termino -γI representa la cantidad de individuos que pasan de la clase de infectados a la clase de protegidos porque se recuperaron. Por último, el término α1S representa la cantidad de individuos vacunados que pasan al compartimiento de infectados. Así, tenemos la siguiente ecuación que describe el cambio en la población de infectados:
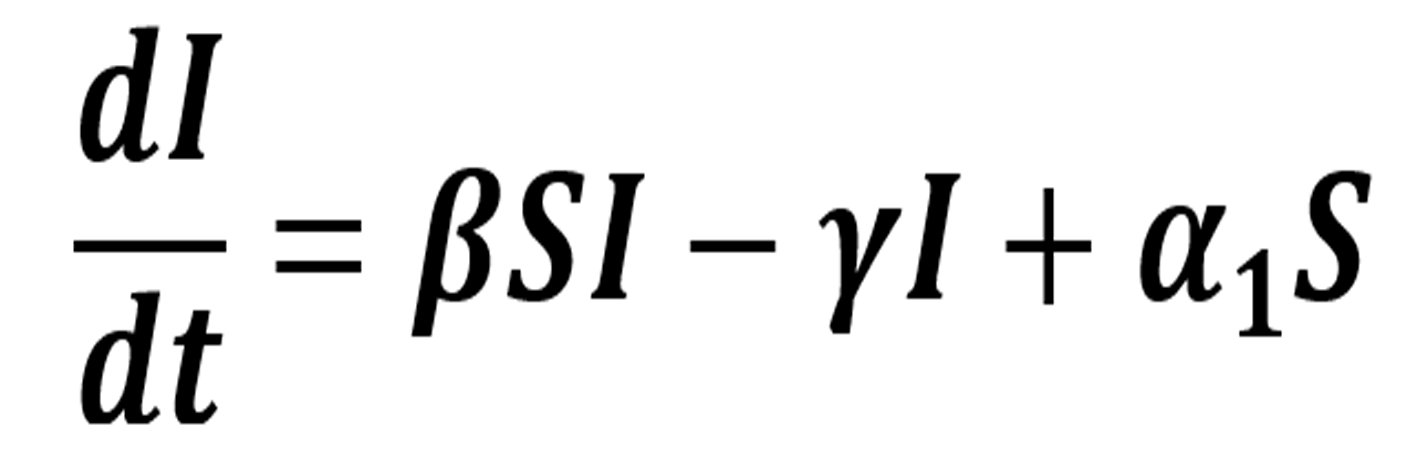
Por otra parte, la variación de individuos protegidos está determinada por la siguiente ecuación:
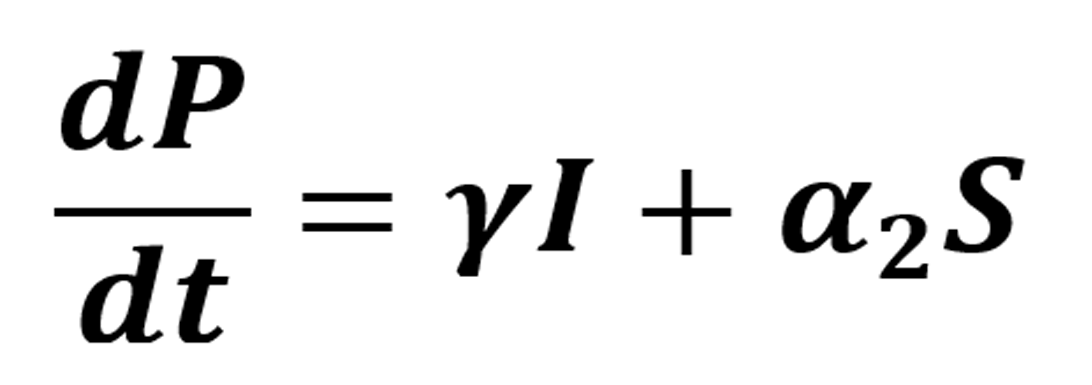
Los puntos críticos del sistema (4), (11) son (0, 0) y 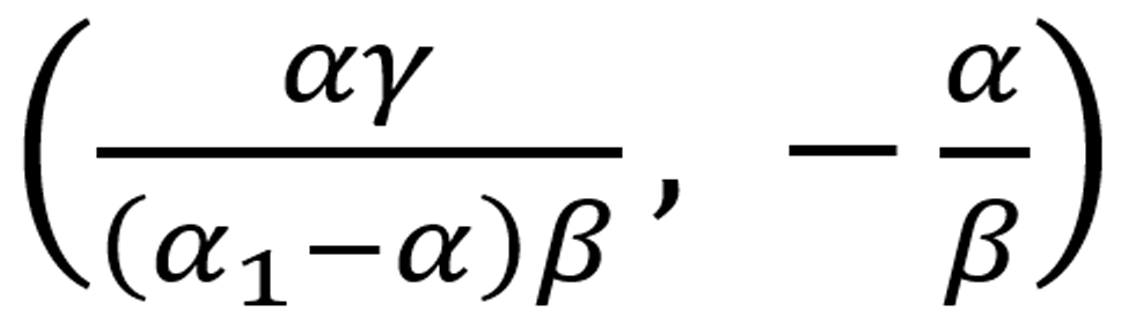 . Como en la primera variante, el origen también corresponde a un atractor. El segundo punto fijo, como en la primera variante, al parecer no tiene interés biológico. Sin embargo, se pueden buscar posibles interpretaciones de dicho punto. Esto puede ser trabajo futuro.
. Como en la primera variante, el origen también corresponde a un atractor. El segundo punto fijo, como en la primera variante, al parecer no tiene interés biológico. Sin embargo, se pueden buscar posibles interpretaciones de dicho punto. Esto puede ser trabajo futuro.
Vamos a considerar que la población total N es constante. Por lo tanto, como en el caso anterior tenemos que P = N - S - I. Así, la dinámica se puede describir con las poblaciones de susceptibles e infectados.
3.1 Primera Variante
Ejemplo 1. Se consideran los siguientes valores para los parámetros del sistema (4) - (6): β = 1, γ = 0.5, α = 0.3
En la Figura 4, se muestra la curva de comportamiento de la primera variante del modelo SIR, en el cual se tienen como valores iniciales una población de susceptibles con 20 individuos y la población de infectados con 2 individuos. Se puede notar que el punto (0, 0) es un atractor, lo cual es congruente con el resultado hallado anteriormente que se deduce de la ecuación (9).
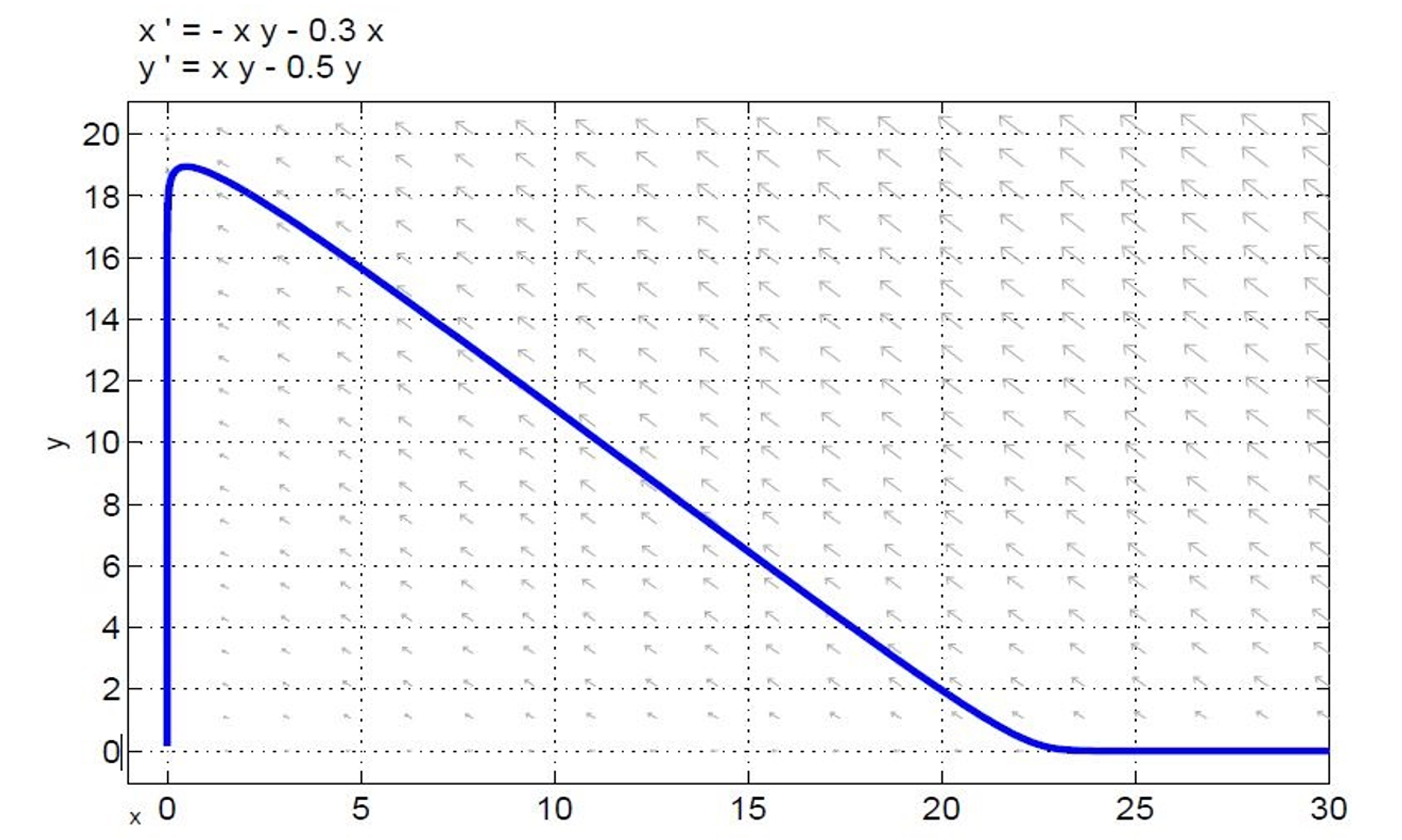
Figura 4. Plano de fase para el ejemplo 1, el cual corresponde a la primera variante del modelo. En este caso, los individuos vacunados pasan al compartimiento de los protegidos
3.2 Segunda Variante
Ejemplo 2. Se consideran los siguientes valores para los parámetros del sistema (4) - (10), (11): β = 1, γ = 0.5, α = 0.3, α1 = 0.1, α2 = 0.2.
La Figura 5 muestra la gráfica del comportamiento de la segunda variante propuesta. De la misma manera que la primera variante, se encuentra (0, 0) es un atractor. También se puede notar que no toda la población de susceptibles es contagiada, ya que una parte de la población obtiene inmunidad debido a la vacuna.
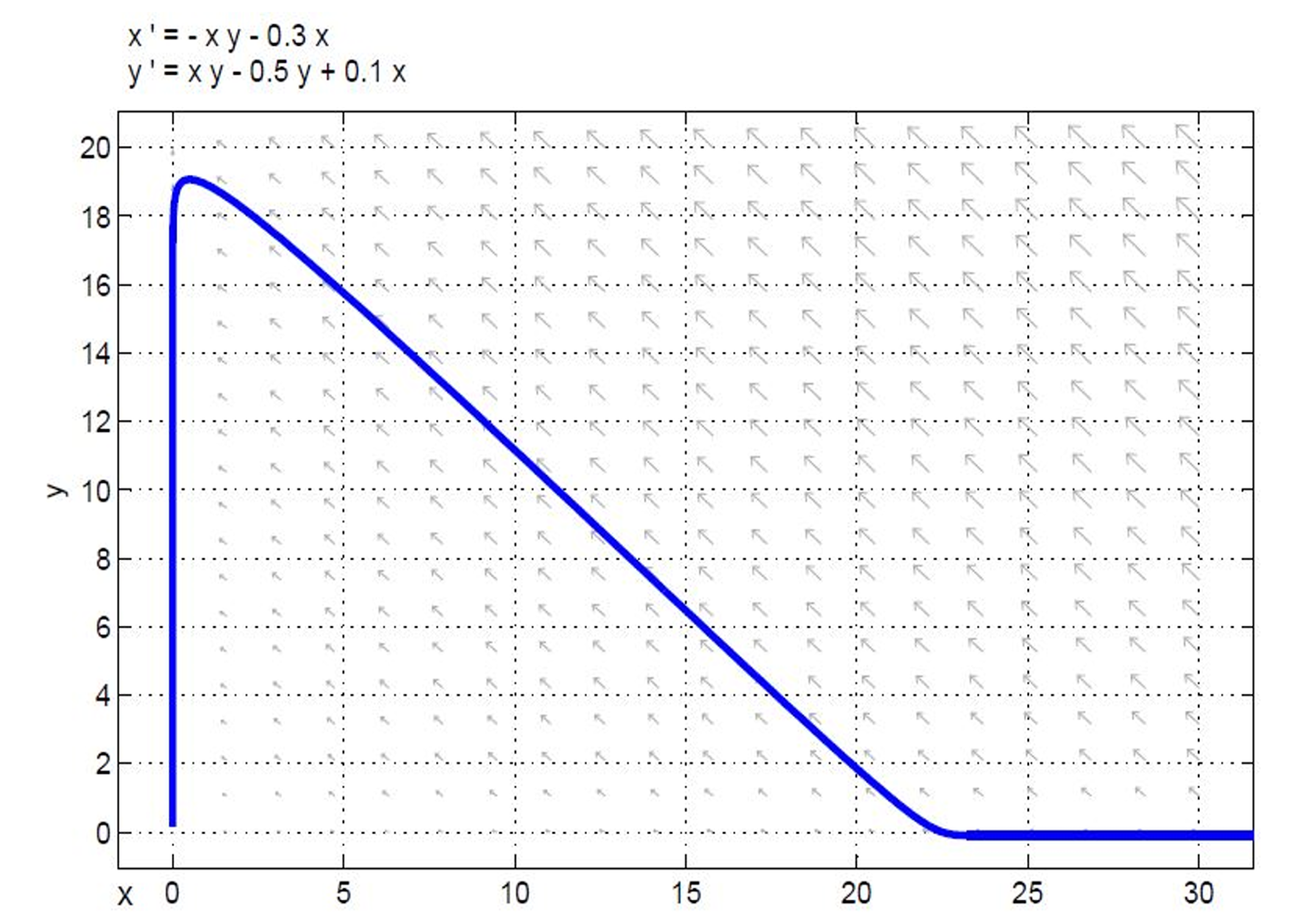
Figura 5. Plano de fase para el Ejemplo 2, el cual corresponde a la primera variante del modelo. En este caso, una parte de los individuos vacunados pasa al compartimiento de los protegidos y otra al de los infectados
Se presentaron dos variantes del modelo SIR, que muestran dinámicas que son plausibles. Se debe determinar a partir de datos cuál de las dos los reproduce mejor. Una vez que se elija un modelo para representar a la dinámica de la epidemia, el paso siguiente consiste en determinar los parámetros del sistema a partir de datos que se tengan de epidemias. En particular, de COVID-19, pues debido a la pandemia actual, se han recopilado muchos datos que pueden utilizarse para validar o ajustar estos u otros modelos [2], [3]. También, ya que se tenga un modelo, podemos ver cuál es la proporción con la que funciona la vacuna. Con ello, se pueden establecer políticas de vacunación que podrían ser más efectivas. Además, se deben incluir en los modelos otros elementos de control como son el uso de cubre bocas, sanitización, confinamiento, actividades controladas, sana distancia, que se reflejarían en el parámetro que mide la tasa de contagio β.