
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 5, 2023
Este documento presenta el modelado y simulación de un detector de ultrasonido Doppler CW para la reconstrucción de alta resolución del perfil de velocidad de flujo sanguíneo de una arteria humana. El sistema utiliza un arreglo de osciladores Van der Pol – Duffing configurados en régimen de intermitencia caótica, y que permite detectar una señal Doppler débil para SNR = -7.5 dB con un error menor a 6%. Los resultados demostraron una alta sensibilidad y resolución para su aplicación en la identificación de patologías como estenosis, la cual está asociada al estrechamiento arterial provocando un incremento en la velocidad de flujo de sangre. En comparación con métodos tradicionales de ultrasonografía Doppler, nuestro arreglo de osciladores en intermitencia promete un mínimo de emisión de potencia que evita efectos bio térmicos, permitiendo largos periodos de exposición.
Palabras claves: intermitencia caótica, perfil de flujo de sangre, detección de estenosis
This document presents the modeling and simulation of CW Doppler ultrasound detector for the reconstruction at high resolution of the blood flow velocity profile of a human artery. The system uses an arrangement of Van der Pol – Duffing oscillators configured in chaotic intermittency which allows detecting weak Doppler signals for SNR = -7.5 dB within less than 6% error. The results demonstrated a high sensitivity and resolution for its application in the identification of a particular case of pathology known as stenosis, which is associated with arterial narrowing that causes an increase in the speed of blood flow. Compared to traditional methods of Doppler ultrasonography, our intermittent oscillator array promises a minimum of power emission that avoids biothermal effects, allowing long exposure periods.
Keywords: chaotic intermittence, blood velocity profile, stenosis detection
El principio de detección mediante ultrasonografía Doppler es aplicado a diversos procedimientos para diagnóstico y prevención; esto incluye instrumentos y métodos tales como: modos A, B, B en escala de grises y M, los cuales operan emitiendo pulsos oscilatorios de corta duración. Para la detección de flujo sangre, el caso más simple llamado Onda Continua Doppler (CW), utiliza dos transductores para transmitir y para recibir el frente de onda CW a una distancia y ángulo dado en dirección del flujo, esta configuración permite detectar tumores o enfermedades circulatorias como estenosis [1]. En los últimos años, se han propuesto varios métodos alternativos para estimar perfiles de velocidad de la sangre en el campo de la investigación médica, por ejemplo el método de Imágenes de flujo Doppler de color (CDFI) [2] que utiliza el desplazamiento Doppler producido por el flujo de sangre para implementar variación de saturación de color, lo que estima de manera "relativa" para la velocidad del flujo, otros instrumentos como la velocimetría láser Doppler (LDV) o flujometría láser Doppler (LDF) se utilizan para medir el flujo en los vasos sanguíneos oculares y otros tejidos [3–6]; sistemas más complejos como los escáneres dúplex en modo B, utilizan formas de onda Doppler pulsante junto con imágenes 2-D para proporcionar en tiempo real la forma, profundidad y posición, mientras que los pulsos Doppler permiten la determinación de la forma y fisiología cardiovascular [7]. Para que una onda emitida sea considerada no invasiva, debe ser irradiada con un mínimo potencia para evitar efectos térmicos dañinos, pero al mismo tiempo debe superar los altos niveles de ruido que pueden añadirse durante la propagación de la onda. Instrumentos comerciales de diagnóstico producen salidas que típicamente caen dentro de rangos de potencia específicos; el modo M por ejemplo, genera una potencia de 3,9 mW, el modo B genera 18 mW, el Doppler pulsado genera 30,7 mW, y el método de flujo de color genera 80,5 mW [8].
2.1 Intermitencia Caótica
El oscilador Van der Pol – Duffing (VDP-Duffing), consiste en una ecuación diferencial no lineal de segundo orden compuesta por la función de amortiguamiento no lineal del oscilador Van der Pol y la función de rigidez no lineal del oscilador Duffing. Este sistema proporciona una dinámica compleja variada que puede exhibir desde oscilaciones periódicas de ciclo límite hasta oscilaciones caóticas cuando se incorporan funciones de forzamiento.
La intermitencia caótica es el mecanismo por medio del cual, un sistema no lineal produce intervalos de tiempo periódicos alternados por estallidos repentinos de caos, para esto, los parámetros del sistema deben estar sintonizados de tal modo que sistema se encuentre en un estado crítico entre ambos estados [9]. A continuación, se presenta una versión modificada del sistema VDP-Duffing propuesto por [10] y modificado para la detección de señales estacionarias como se muestra en la fórmula (1)
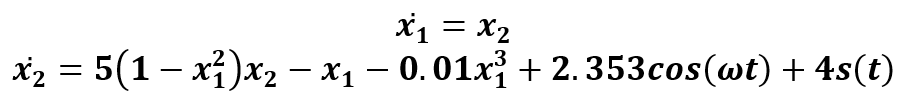
donde s(t)=F1 cos(ω1 t)+η(t) es una señal débil de amplitud pequeña dada por F1=0.05 y frecuencia ω1, la cual se encuentra sometida a ruido blanco con distribución Gaussiana η(t). La estimulación de la señal pequeña perturbará al sistema, lo que provocará saltos entre estados caóticos y periódicos como se muestra en la Figura 1
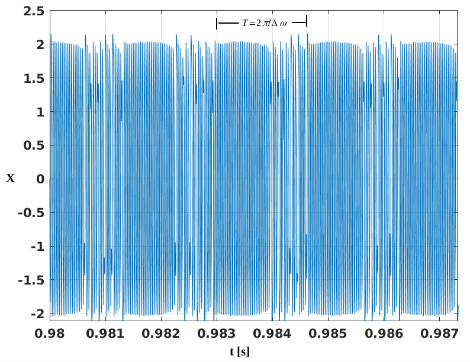
Figura 1. Secuencia en dominio del tiempo mostrando saltos entre el estado caótico y periódico
Aquí, la frecuencia de la señal débil está contenida en los periodos de intermitencia, por lo que puede estimarse a través de la ecuación T=2 π⁄Δω, tal que Δω=|ω-ω1 | es la diferencia absoluta entre la frecuencia de la función de forzamiento de la ecuación (1) y la frecuencia de perturbación; esta diferencia deberá ser mínima para preservar los periodos de intermitencia, por ejemplo Δω < 0.07.
2.2 Detección de señal Doppler
El sistema visto en la sección anterior es completamente asequible para su implementación como detector cuando la perturbación débil es estacionaria; sin embargo, cuando la perturbación es no estacionaria en frecuencia como ocurre con señales tipo Doppler, el sistema no será capaz de responder a los cambios de frecuencia, esto se debe a la restricción dada por Δω < 0.07, lo que limita al sistema en ancho de banda. Para superar este inconveniente, se propone el esquema de detección adaptativo de la Figura 2, que incluye un arreglo de osciladores VDP-Duffing [11]. Cada oscilador está sintonizado a una frecuencia diferente ligeramente encima y por debajo de una frecuencia inicial central, que para distinguir los períodos intermitencia más eficientemente, se obtiene la correlación cruzada entre la secuencia intermitente. Posteriormente, se miden todos los periodos intermitentes de los cinco osciladores, obteniendo un promedio estadístico para estimar la frecuencia Doppler. Una vez estimada la frecuencia en la n-ésima ventana se reemplaza inmediatamente como la nueva frecuencia central para el cálculo de la siguiente ventana en un proceso adaptativo, este proceso se repite hasta que todas las N ventanas están completas, cuyo resultado será un arreglo de frecuencias en el dominio del tiempo.
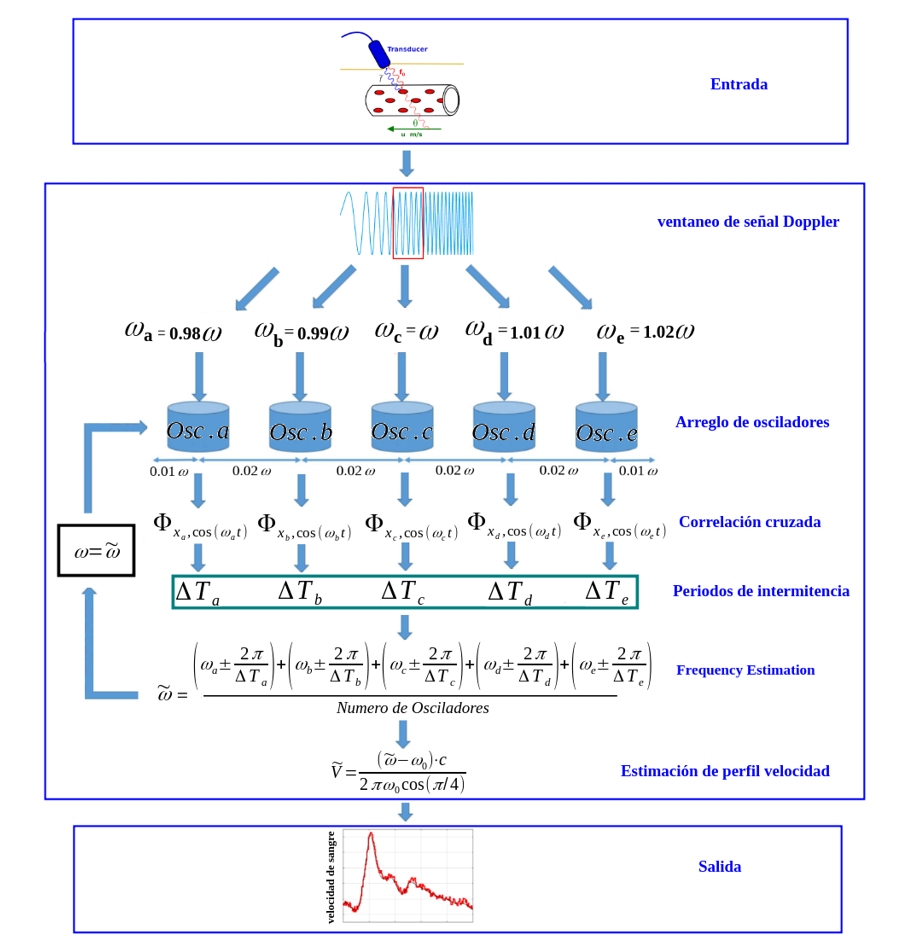
Figura 2. Esquema de solución para la detección y reconstrucción de perfil de flujo sanguíneo
3.1 Esquema experimental
Para llevar a cabo los experimentos, dos tipos de señales Doppler fueron sintetizadas: 1) el perfil de velocidad de la sangre correspondiente a un individuo sano, y 2) el perfil de velocidad de la sangre de una arteria con estenosis. Estas señales se generaron a partir de una muestra aleatoria de perfiles de sangre reales [12-13], y luego se reconstruyeron a través de un proceso de ajuste de curvas polinómicas. Cuando la señal de la fuente se aplica al tejido, sufre atenuación y desvanecimiento, principalmente debido a los diferentes compuestos en el tejido y la sangre [14], además, las arterias con estenosis pueden derivar en un flujo sanguíneo turbulento; estos factores hacen que la medición de flujo no invasiva "in vivo" sea un desafío, y que la señal Doppler detectada esté sujeta a altos niveles de ruido. Para simular las condiciones antes mencionadas, las señales Doppler de prueba son contaminadas con ruido blanco Gaussiano aditivo para diferentes SNR que van desde 0 a -10 dB. La configuración experimental completa se muestra en la Figura 3.
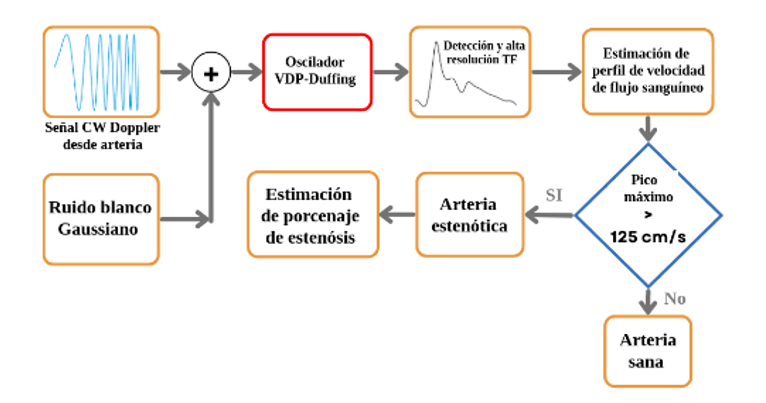
Figura 3. Esquema experimental en la reconstrucción del perfil de flujo sanguíneo para la identificación de estenosis
Para implementar correctamente el esquema adaptativo mencionado en la sección anterior, se debe considerar lo siguiente: 1) la diferencia de frecuencia se establece en ∆ω/ω = 0.07 lo que permite una mejor estimación de las pequeñas variaciones de frecuencia (como como el caso de nuestra señal Doppler bajo estudio), 2) después de aplicar la correlación cruzada para la n-ésima ventana, se localizan los máximos locales y se mide el lapso de tiempo entre ellos 3) se considera un traslape de ventana del 50% para reducir la dispersión de frecuencia durante su estimación, lo que a su vez aumenta la resolución TF [9].
3.2 Acondicionamiento de la señal
La Figura 4 muestra el esquema Doppler CW propuesto por [15] para la detección de la velocidad de la sangre en una arteria; el emisor envía una onda de ultrasonido frontal f0 en dirección al flujo con un ángulo de incidencia θ respecto a la superficie de la piel, y cuando la onda es reflejada por la sangre, el detector percibe un cambio en la frecuencia ∆f dado por la fórmula (2)
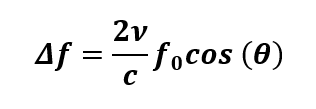
donde ν es la velocidad del flujo sanguíneo, c es la velocidad del sonido sobre tejidos blandos que van desde 1540 m/s a 1600 m/s [18], y θ conocido como el ángulo de insonación que tiene un valor aproximado de 45° ± 4° [16-17].
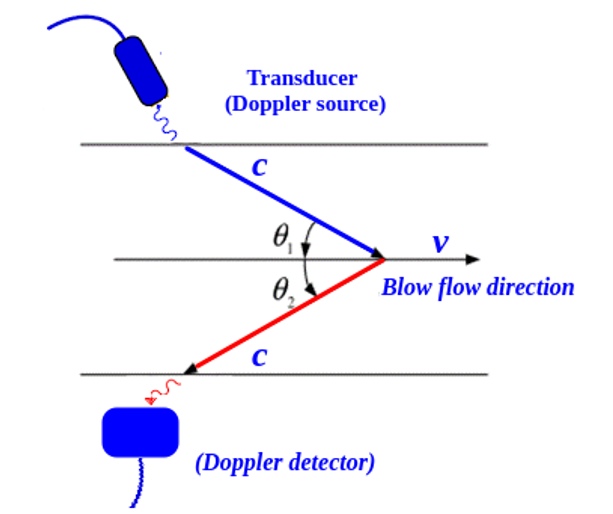
Figura 4. Principio de medición a través de ultrasonido Doppler de onda continua
Al considerar la velocidad del sonido en el tejido c = 1570 m/s, la frecuencia del transmisor ultrasónico Doppler f0= 30 KHz, el ángulo de incidencia θ = 45° y supongamos la velocidad de la sangre en la arteria carótida en el intervalo de 25-125 cm/s. Con estos datos, podemos estimar las variaciones de frecuencia en un intervalo desde 4.053 Hz y 21.61 Hz. Además, para simular las condiciones de dispersión y acumulación de ruido en la señal durante su recorrido hacia el transductor, se incluye ruido blanco gaussiano a través de la relación señal ruido como se muestra en la fórmula (3)
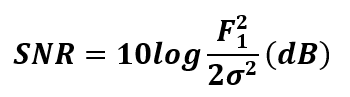
donde σ2 es la varianza de todo posible ruido agregado a la señal Doppler. Para obtener la solución numérica del sistema VDP-Duffing, se emplea el método Runge-Kutta de cuarto orden y paso fijo.
3.3 Resultados
Para evaluar el desempeño del sistema, se aplica el método de Monte Carlo para promediar 50 iteraciones con diferentes casos de ruido para una misma SNR, las cuales serán sumadas a la señal Doppler bajo estudio, y nos dará una estimación del perfil de velocidad de la sangre. Este proceso se reproduce con diferentes SNR de 0 a -10 dB para evaluar la sensibilidad del sistema.
Así, la Figura 5a muestra la reconstrucción del perfil de velocidad de la sangre para un individuo sano, y en la Figura 5b la reconstrucción de perfil de flujo de sangre típica de estenosis, en ambos casos cuando la señal Doppler se contamina con ruido para una SNR = -10 dB; en color negro se muestra los perfiles de flujo de sangre real en cada caso.
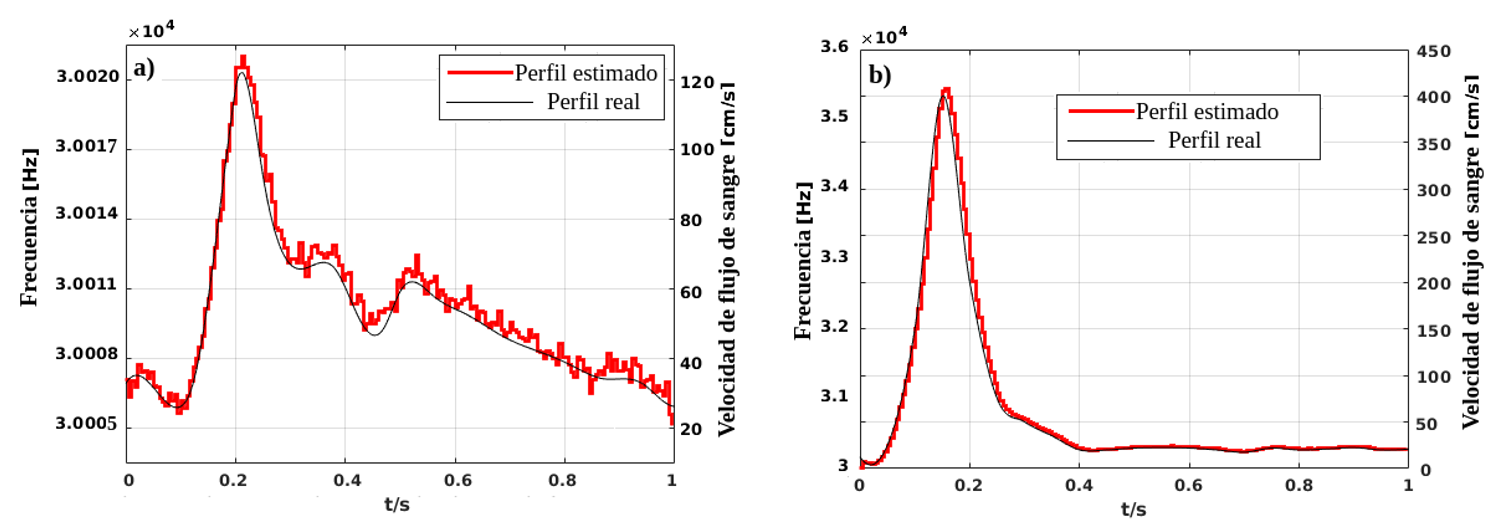
Figura 5. Reconstrucción de perfil de flujo sanguíneo para SNR=-10dB, a) perfil sano, b) perfil con estenosis
Para una mejor referencia, en la Tabla 1 se muestran los resultados de detección de perfil de flujo sanguíneo como un error en función de distintas SNR, este error se calcula como el porcentaje de error medio absoluto entre la frecuencia estimada y la frecuencia real en la forma %error = 100 * {|ωreal - ωestimada | /ωreal}.
Tabla 1. Evaluación de sistema en diversos escenarios de ruido
| SNR | 0.dB | -5 dB | -7.5 dB | -10 dB |
|---|---|---|---|---|
| %error | 5.5% | 5.58% | 6.25% | 6.44% |
Puesto que la amplitud de la señal acústica emitida puede disminuir como una función de la profundidad de penetración en el tejido [8], la potencia media se estima con la fórmula (4):
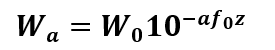
Donde a es el coeficiente de atenuación debido a la dispersión de la señal dentro del tejido, que para la mayoría de los casos es 0.03 np/cm-MHz; f0 es la frecuencia de operación (30 Khz); z es la profundidad de penetración; W0 es la potencia de emisión desde la fuente. Entonces, al tener en cuenta la potencia media de la fuente en W(0)= 1.8 mW, que es equivalente a la amplitud de la función de perturbación, la ecuación 4 indica que la potencia promedio percibido por el transductor es W0.03= 1.7675 mW, lo que comprueba una atenuación mínima.
Además, el índice térmico (TI) definido como TI=W0 /(210/f0 ), establece que para cualquier método de ultrasonido Doppler, este valor debe cumplir TI ≤ 1 para evitar efectos térmicos (AIUM/NEMA 1992) [8]. Para nuestro sistema, el valor TI = 0.18, por lo tanto, aseguramos condiciones confiables de funcionamiento.
En este trabajo se emplea un sistema VDP-Duffing en régimen de intermitencia, incorporado en un arreglo adaptativo de osciladores para la detección de señales no estacionarias bajo condiciones severas de ruido. El sistema se empleó como un detector de señal Doppler de onda continua que permitió identificar los cambios de velocidad de la sangre en una arteria humana; esto también favoreció a la identificación de un caso de patología circulatoria conocido como estenosis. Para evaluar el desempeño del sistema, dos señales correspondientes al perfil de flujo de sangre Doppler sano y estenótico fueron sintetizadas, para ambos casos se agregó ruido blanco Gaussiano simulando las condiciones que experimenta la señal en su trayecto desde la fuente hasta el receptor. La alta resolución tiempo-frecuencia de nuestro sistema permitió la estimación de los cambios de velocidad de flujo de sangre, así como la reconstrucción del perfil de flujo aun cuando la intensidad de ruido sea severa. A diferencia de instrumentos comerciales ya mencionados, nuestro sistema requiere una potencia de emisión de 1.25 mW, con índice térmico TI = 0.18, lo que representa mínimos efectos térmicos invasivos.