
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
En este trabajo se presenta un estudio sobre la síntesis de un mecanismo de extremidad inferior para un robot bípedo. El enfoque propuesto consiste en analizar la metodología que se implementará para generar un mecanismo adecuado, con énfasis en replicar la marcha humana. Los objetivos incluyen analizar los aspectos anatómicos y biomecánicos de la locomoción humana, sintetizar el diseño mecánico para replicar la marcha humana utilizando herramientas de diseño asistido por computadora y modelar el sistema cinemático y dinámico necesario para la reproducción de la marcha. El mecanismo propuesto es un sistema de cuatro barras tipo plano, que se conforma de enlaces fijos, de conducción, acopladores y seguidores, diseñados para imitar los movimientos del miembro inferior humano.
Palabras claves: Mecanismo, marcha humana, sub-actuado
This paper presents a study on the synthesis of a lower limb mechanism for a bipedal robot. The approach to follow consists of analyzing the methodology to be followed to generate an appropriate mechanism, with emphasis on replicating human gait. The objectives include analyzing the anatomical and biomechanical aspects of human locomotion, The study of the mechanical design for the reproduction of human gait using computer-aided design tools and modelling the kinematic and dynamic system required for the reproduction of the march. The proposed mechanism is a four-bar flat type system, which consists of fixed links, driving, couplers and followers, designed to mimic the movements of the human lower limb.
Key words: Mechanism, Human gait, Underactuated
Los robots bípedos humanoides han sido usados en una amplia gama de aplicaciones, debido a su diseño y función principal, que consiste en desplazarse utilizando dos extremidades inferiores que se asemejan a las piernas humanas.
Las aplicaciones de los robots bípedos van desde el área industrial, de servicio, asistencia del hogar, investigación, médica, etc. En el campo de la robótica han surgido muchos proyectos internacionales de desarrollo de robots humanoides adaptados a entornos domésticos o laborales que trabajan como robots de servicio, puesto que pueden llegar a tener mejor maniobrabilidad y facilidad para moverse en entornos con superficies irregulares, escaleras, etc. [1].
Para el diseño de estos robots se emplea el uso de diversas áreas de conocimiento como la mecánica, desarrollo de software y biomecánica las cuales serán esenciales para la propuesta del mecanismo. La mecánica constituye una rama fundamental de la física que se dedica al estudio tanto del movimiento como del equilibrio de objetos, además de las fuerzas que ejercen influencia sobre estos [2]. En este contexto, emplearemos diversas disciplinas de la mecánica para comprender, analizar y afrontar los fenómenos físicos relacionados con la locomoción y la estabilidad de los robots humanoides.
En este caso particular, proponemos un mecanismo del tipo plano sub-actuado, lo que implica que el número de actuadores será inferior al número de grados de libertad (GDL) o, en este contexto, al número de articulaciones presentes en el mecanismo [3]. Esta categoría de robots bípedos resulta extremadamente útil, ya que nuestro objetivo es desarrollar un mecanismo que funcione eficazmente con un único actuador, a diferencia de los robots bípedos totalmente actuados, que suelen contar con un actuador en cada una de sus articulaciones móviles.
Para el desarrollo del mecanismo es necesario conocer cómo funciona el modelo cinemático de la marcha humana, al comprenderlo es posible aplicar dichos principios para diseñar un mecanismo eficiente capaz de reproducir un patrón de movimientos semejante. Para este estudio se usarán como apoyo algunas herramientas como el uso del software GeoGebra® para el análisis cinemático de posición.
2.1 La marcha humana
La marcha humana es una forma de locomoción bipodal con actividad alternante de los miembros inferiores y mantenimiento del equilibrio dinámico [4]. Esta acción consiste en una secuencia de acciones en constante repetición para conseguir un desplazamiento como se observa en la Figura 1. Arbitrariamente se toma como inicio del ciclo el contacto de un miembro con el suelo, de modo que su final se alcanza cuando el mismo miembro vuelve a contactar con el suelo [4].

Figura 1. Tiempos de la marcha en el plano sagital [5]
Como se muestra en la Figura 1, el proceso consiste en un apoyo bilateral, donde ambos pies están en contacto con el suelo, sosteniéndose tanto en el talón como en el antepié. Luego, pasamos a un apoyo unilateral, donde el cuerpo se sostiene sobre una sola pierna, adoptando una posición plantígrada. Mientras tanto, la pierna contraria se mantiene suspendida en el aire y realiza un movimiento de balanceo hacia adelante hasta que vuelve a tocar el suelo, apoyándose en el talón. Este paso proporciona un segundo apoyo bilateral, hasta que el pie que estaba en movimiento de balanceo regresa a la posición plantígrada, permitiendo así la repetición del ciclo.
Los tiempos de la marcha humana son estudiados desde la vista el plano atómico sagital, el cual puede definirse como un plano imaginario que divide el cuerpo humano en mitades derecha e izquierda. Este plano se extiende longitudinalmente de manera vertical y atraviesa el cuerpo desde la parte frontal hacia la parte posterior, dividiéndolo en dos secciones simétricas [6]. En este plano podemos encontrar los movimientos de flexión, extensión, dorsiflexión, flexión plantar e hiperextensión. Estos movimientos se definen por el acercamiento y separación de los huesos entre sí, lo que resulta en una reducción o aumento del ángulo en una articulación definida.
Al examinar el patrón de movimiento que se presenta durante la marcha humana, nos centramos en el comportamiento angular de las articulaciones el cual desempeñan un papel crucial en este proceso. En las siguientes gráficas podremos observar en detalle cómo se desenvuelve dicho comportamiento angular, el cual se describe conforme a la extensión y flexión de las articulaciones. En las gráficas de la Figura 2 y 3 se expone la extensión y flexión de la articulación de la cadera y la rodilla respectivamente con respecto al porcentaje del ciclo de la marcha. En la Figura 4 podemos observar el comportamiento angular del tobillo, esta gráfica a diferencia de las anteriores se enfoca en la flexión plantar y la dorsiflexión con respecto al porcentaje de ejecución de la marcha humana.
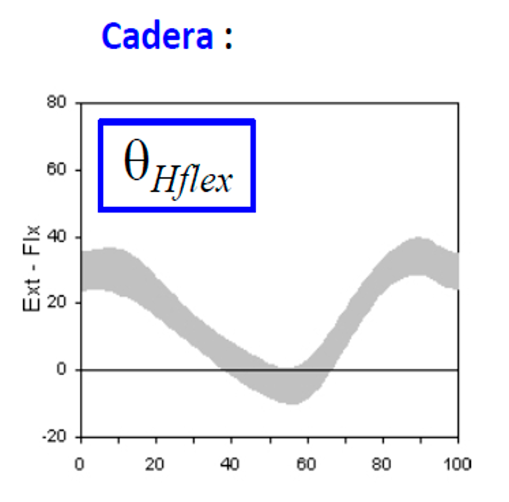
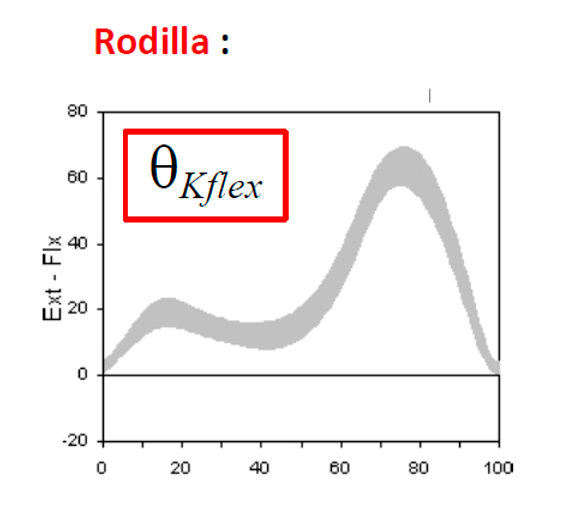
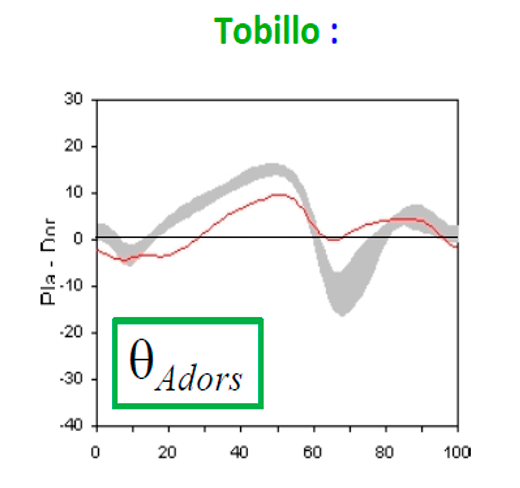
Figura 2. Comportamiento angular de la cadera [7].
Figura 3. Comportamiento angular de la rodilla [7].
Figura 4. Comportamiento angular del tobillo [7].
El mecanismo que simbolizará las articulaciones inferiores del cuerpo humano se representa mediante un sistema de cuatro barras, lo que facilita el análisis cinemático durante la marcha. Este sistema está compuesto por cuatro elementos conectados que representan la cadera, la rodilla y finalizan en la región del talón. A continuación, en la Figura 5, se presenta una imagen que ilustra esta propuesta de mecanismo.
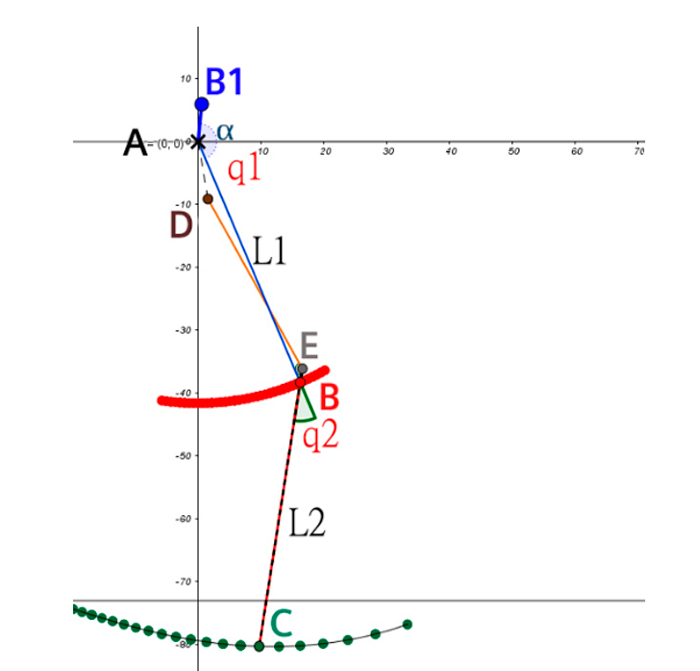
Figura 5. Propuesta mecanismo de cuatro barras que simulara la marcha humana
En este diseño, el eslabón AD se establece como fijo representando la cadera. El eslabón motriz está representado por los puntos B1, A, B, que representan el movimiento que seguiría el muslo anterior. El eslabón acoplador es DE, que representa el muslo posterior. Por último, el eslabón seguidor es BC, que simula el comportamiento desde la rodilla hasta el tobillo. También se puede observar la trayectoria del punto B en color rojo, que representa la articulación de la rodilla. La trayectoria del punto C en color verde representa la trayectoria de la articulación del talón. Estas trayectorias se generan en función del movimiento actuado del ángulo α el cual simula el movimiento de la cadera en el eje anatómico sagital.
La estructura mostrada en la Figura 5 también puede describirse como un mecanismo de cuatro barras de péndulo. Este mecanismo está compuesto por cuatro barras rígidas conectadas entre sí por cuatro pares cinemáticos de revoluta. Los eslabones tienen un movimiento rotatorio puro alrededor del eje de unión. Permitiendo utilizar un control de posición sobre las articulaciones de interés, enviando esta información a un controlador.
3.1 Cinemática del robot
La cinemática de un robot estudia el movimiento de este con respecto a un sistema de referencia preestablecido. De esta forma se encarga de realizar una descripción del movimiento que efectúa un robot o mecanismo sin considerar fuerzas externas que actúan sobre el cómo la gravedad, su principal objetivo es describir la posición y orientación del robot.
Existen dos métodos para describir la cinemática de un robot:
En este caso nos centraremos en el primer método, ya que gracias a GeoGebra® tenemos la información necesaria para llevarlo a cabo. La articulación de la rodilla q2 está directamente relacionada con el ángulo de entrada q1 del único actuador. Las longitudes de las palancas Ln se calculan a partir de la distancia entre los puntos de pivote y los extremos de las palancas. La función f(q1) obtenida mediante regresión polinomial describe la cinemática del comportamiento entre los eslabones en relación con el movimiento mecánico. Esto permite establecer un rango de operación funcional para el sistema de dos articulaciones, simplificando así la cinemática del sistema sub-actuado.
Considerando la función f(q1) ahora podemos describir la cinemática de las articulaciones en términos de una sola variable y simplificar el análisis, considerando lo de la siguiente forma:
sabiendo que:
El sistema cinemático del mecanismo de cuatro barras se conformaría por las siguientes matrices:
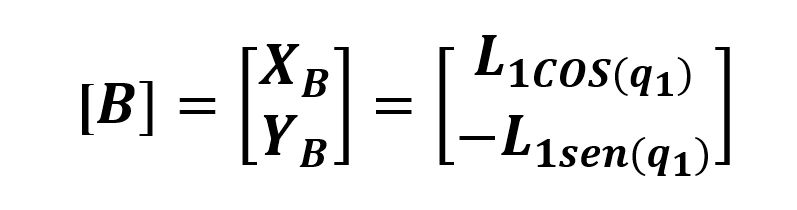
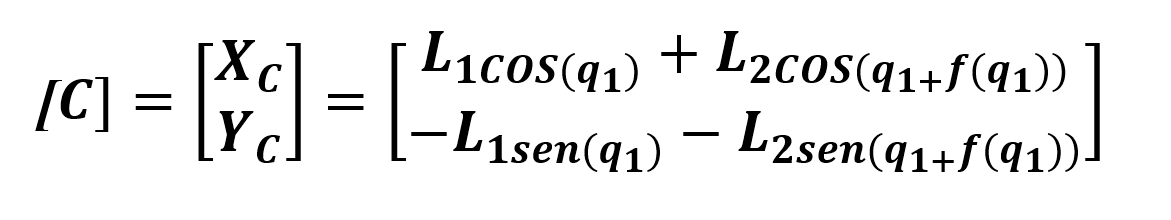
La matriz que define la posición del punto B se construye a partir de sus coordenadas (XB, YB) y la descomposición de las fuerzas que actúan sobre él en la dirección del vector correspondiente. El ángulo de este vector se representa como q1 y la longitud del eslabón que une el origen al punto B se denomina L1. Cabe destacar que la orientación del punto B en el eje Y es negativa debido a que se encuentra en el cuadrante cuatro del plano cartesiano.
La posición del punto C se describe mediante el vector B1B, también conocido como L1, el cual replica el movimiento oscilatorio del punto B. Este movimiento genera una variación en el ángulo q2, considerado complementario al ángulo q1 del primer eslabón L1. Con base en esto, se establece un nuevo sistema de coordenadas para el segundo eslabón. Dado que se conoce la relación entre q2 y q1, se reemplaza este valor en la ecuación por f(q1), lo que permite determinar la posición del segundo eslabón BC, denominado L2 en la ecuación.
Las ecuaciones revelan que el punto B ejecuta un movimiento oscilatorio de tipo pendular alrededor del origen. Esta trayectoria circular es consecuencia de una transformación de rotación simple y está confinada dentro de los límites geométricos impuestos por los demás eslabones del mecanismo, por otro lado, la función f(q1) introduce un acoplamiento entre los movimientos de B y C, como se muestra en las ecuaciones, haciendo que la trayectoria de C sea más compleja y dependiente de las posiciones angulares de ambos eslabones. La forma y tamaño de la curva descrita por C varían en función de los valores de q1 y q2.
En este trabajo se presenta un estudio sobre la síntesis de un mecanismo de extremidad inferior para un robot bípedo, con el objetivo de replicar la marcha humana. A diferencia de otros estudios que emplean mecanismos más complejos, el enfoque propuesto en este trabajo se basa en un análisis detallado de la biomecánica del ser humano para desarrollar un mecanismo simplificado con una sola articulación actuada. Esta simplificación permite formular un análisis cinemático adecuado que nos describa el comportamiento del mecanismo matemáticamente, también el modelo cinemático desarrollado permite simular de manera detallada el movimiento del mecanismo, lo que facilita la optimización del diseño y la identificación de posibles áreas de mejora. Futuras investigaciones se centrarán en la implementación experimental del mecanismo, así como en la incorporación de elementos de control para lograr una marcha más robusta y adaptable.