Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud
Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
Se tiene interés en aplicar el efecto Talbot para medir distancias a través de los laparoscopios. Este efecto consiste en la generación de imágenes repetidas de un objeto periódico, llamadas autoimágenes, cuando se ilumina con luz monocromática coherente. Para ondas planas estas autoimágenes se producen a distancias equidistantes. Investigaciones previas han demostrado la utilidad del efecto Talbot en la medición de objetos escalonados [1]. Para evaluar la propuesta, se simuló en el laboratorio un relevador de laparoscopio con un sistema óptico equivalente, usando una rejilla de difracción como objeto periódico. Los resultados preliminares indican que, a distancias cercanas del sistema colimador, la separación entre autoimágenes se conserva tras pasar por el relevador, confirmando la viabilidad de esta propuesta.
Palabras clave: Efecto Talbot, laparoscopio, relevador
There is interest in applying the Talbot effect to measure distances through laparoscopes. This effect consists of the generation of repeated images of a periodic object, called self-images, when illuminated with coherent monochromatic light. For plane waves, these self-images occur at equidistant distances. Previous research has demonstrated the usefulness of the Talbot effect in measuring stepped objects [1]. To evaluate the proposal, a laparoscope relay with an equivalent optical system was simulated in the laboratory, using a diffraction grating as a periodic object. Preliminary results indicate that, at close distances from the collimator system, the separation between self-images is preserved after passing through the relay, confirming the viability of this technique in laparoscopes.
Keywords: Talbot effect, laparoscope, relay
Los endoscopios son instrumentos cruciales en la medicina, ya que permiten la observación y manipulación de regiones internas del cuerpo humano [2]. El sistema formador de imagen de un endoscopio está compuesto por una fuente de luz, un cable de luz, un telescopio, una cámara y un monitor de video. Los telescopios pueden ser rígidos o flexibles; este estudio se enfoca en los telescopios rígidos [3]. En la Figura 1 se muestra una imagen del telescopio de un laparoscopio y sus elementos básicos. Este se compone principalmente de un objetivo, encargado de formar y magnificar la imagen, una serie de relevadores que la transmiten, y un ocular que permite observarla directamente con el ojo humano o a través de un monitor de video. En esencia, la composición del sistema óptico del telescopio de este laparoscopio es similar a la de cualquier tipo de endoscopio.
Figura 1. Sistema óptico de un laparoscopio
Los endoscopios se nombran y clasifican según su aplicación. Por ejemplo, el laparoscopio, mencionado anteriormente se utiliza para examinar la cavidad abdominal y pélvica. Existen otros tipos como el artroscopio, que se emplea en articulaciones como rodillas, hombros, cadera, tobillos, etc. [4]. En la Figura 2 se presenta la imagen de una artroscopía de rodilla donde se mide su anatomía para elegir una prótesis adecuada para su reconstrucción. Sin embargo, esta técnica resulta invasiva, ya que implica la inserción de una regla artroscópica adicional [5].
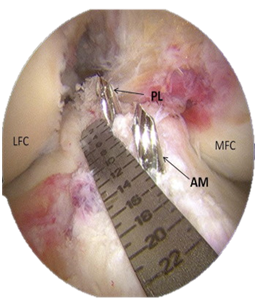
Figura 2. Artroscopía de rodilla [6]
Es de interés poder medir distancias a través de un endoscopio de forma menos invasiva empleando el fenómeno de autoimágenes. Como ya se mencionó en el resumen este fenómeno consiste en la reproducción repetida, sin lentes, de imágenes de un objeto periódico que es iluminado por un haz de luz plano, coherente y monocromático [1].
Existen algunos laparoscopios que permiten acoplar una fibra óptica, para visualizaciones simultaneas tanto con el ojo humano como en una pantalla. En estos equipos es posible añadir un divisor de haz similar a los que se utilizan en microscopia para visualización simultánea. Se tiene la intensión de utilizar este aditamento, para enviar la imagen de una rejilla (objeto periódico) y se pueda superponer con la imagen bajo prueba. Es decir, la rejilla está fuera del laparoscopio y la imagen de esta se mandaría a través del sistema formador de imagen. Se ajustaría el periodo de esta para que los patrones de alto contraste se superpongan con la imagen bajo análisis [6, 7].
Investigar la viabilidad de utilizar el efecto Talbot para medir distancias a través de un endoscopio, en particular de un laparoscopio, a partir de la simulación en laboratorio del relevador con el que están diseñados. Esta prueba de concepto permitirá seguir con la adaptación del efecto Talbot a la medición de profundidades.
Al iluminar un objeto periódico, que consiste en distribuciones de zonas negras y transparentes conocidas como rejillas de difracción, con un haz de luz plano, coherente y monocromático, las imágenes repetidas de la rejilla se generan a distancias equidistantes determinadas por la distancia:
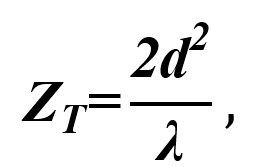
donde d es el periodo de la rejilla y λ la longitud de onda. A estas imágenes se les conoce como autoimágenes (o también conocidas como autoimágenes “positivas”) y se encuentran en nZT donde n es un número entero. Además, en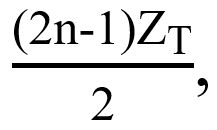 
se encuentran las autoimágenes "negativas", que son una réplica de la imagen de la rejilla, aunque desplazada medio periodo. Así, partiendo de la ecuación 1, la separación entre autoimágenes “positivas” y “negativas” viene dada por [8]:
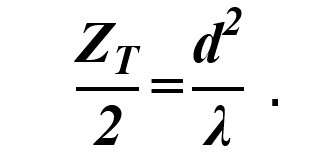
La representación de este fenómeno se puede visualizar en la Figura 3, en donde una rejilla de Ronchi es iluminada con ondas planas generadas al colimar una fuente de luz láser. Las autoimágenes “positivas” se presentan en color naranja y las autoimágenes “negativas” en color verde. Sin embargo, en esta primera propuesta se utilizó únicamente la primera autoimagen, es decir, n=1. Esto implica, ajustar el periodo de la rejilla para que la zona bajo prueba coincida con la distancia entre dos autoimágenes.
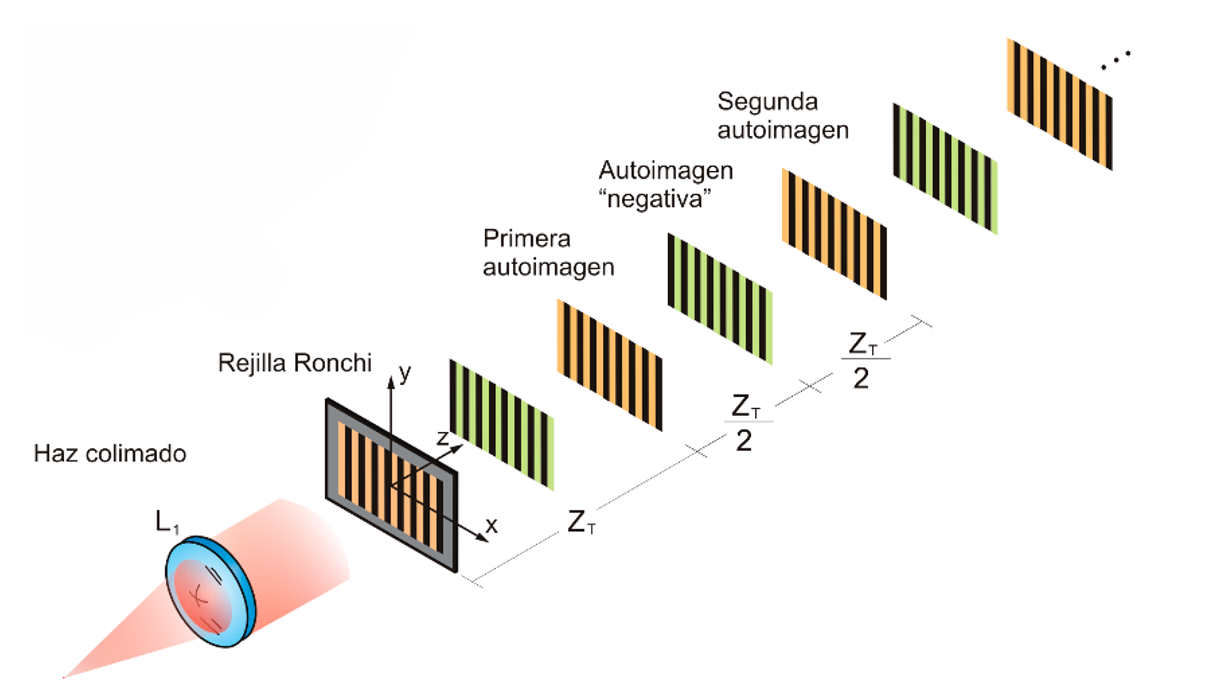
Figura 3. Representación del efecto de autoimágenes o efecto Talbot
Como se mencionó antes, para poder probar la viabilidad de la propuesta, se simuló el relevador de un endoscopio, o bien del laparoscopio de la Figura 1, que consiste en un sistema de transmisión de imagen conocido como 4F, tal y como se muestra esquemáticamente en la Figura 4 [9]. El sistema óptico compuesto consiste en iluminar una rejilla de Ronchi con un haz de luz láser colimado (ondas planas). La rejilla se coloca en el foco de la lente L2, conocida como lente transformadora [9]. Al pasar a través de esta lente, se obtiene la transformada de Fourier bidimensional de la rejilla en su plano focal. A continuación, se coloca la lente L3, cuyo foco anterior debe coincidir con el de L2. Esta lente es responsable de realizar nuevamente la transformada, de modo que, se puede observar la imagen de la rejilla en el plano a la distancia focal de L3. La imagen de la rejilla es una rotación de 180° en dirección antihoraria con el eje óptico como eje de rotación de la rejilla de Ronchi, es decir, el sistema de referencia se localiza tal que la estructura periódica sea una función impar. Las lentes L2 y L3 se eligen con la misma distancia focal para simplificar el arreglo experimental. Se verifica que la reproducción de autoimágenes a la distancia 
se mantiene al pasar por el relevador.
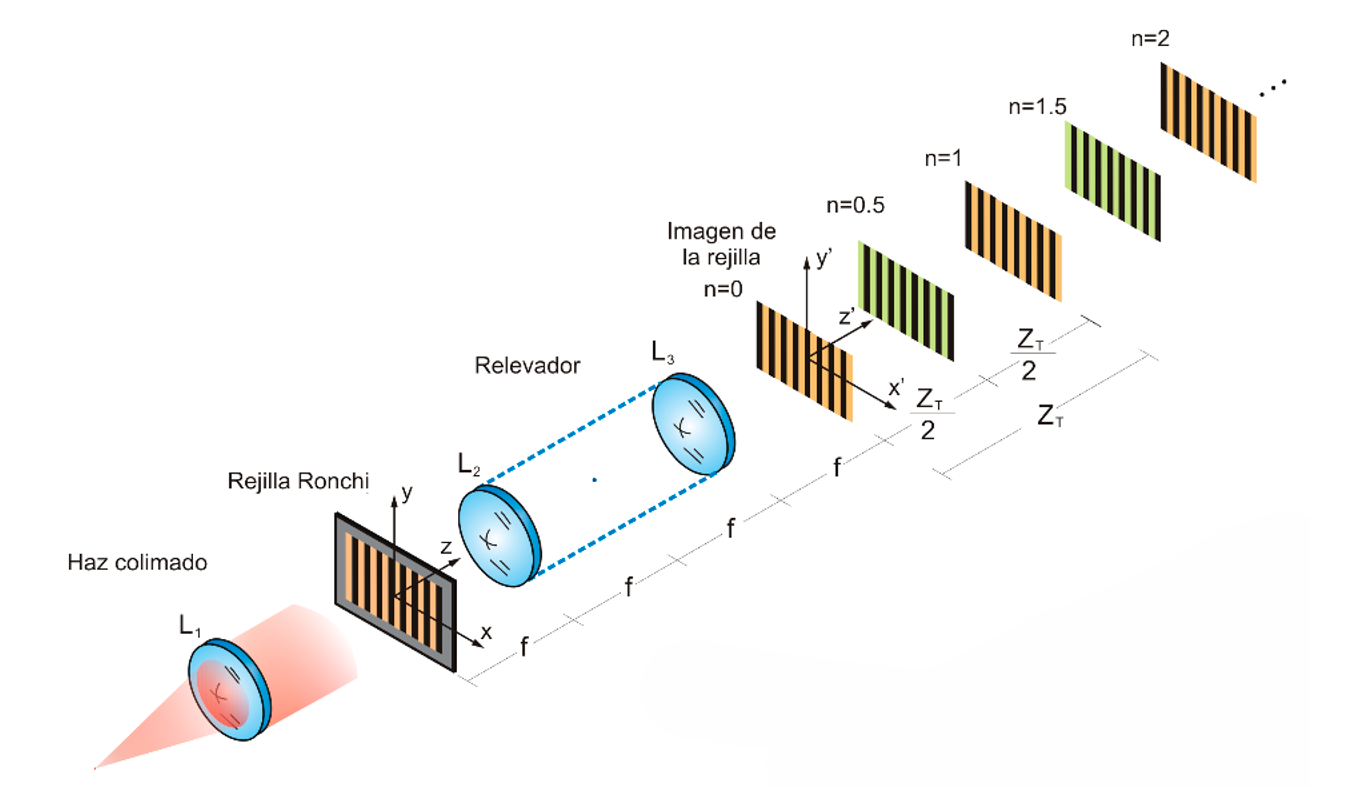
Figura 4. Diagrama del arreglo experimental para la simulación del relevador de un laparoscopio convencional
Para el sistema se utilizó una rejilla de Ronchi de 10 ciclos por milímetro (Figura 5a y 5b), un haz de luz colimada con λ = 633 nm y dos lentes simples biconvexas con un diámetro de 5 cm y una distancia focal de 15 cm.
Figura 5. a) Rejilla Ronchi de 10 ciclos por milímetro. b) Imagen de la rejilla tomada con cámara CCD en un sistema con una lente a dos veces del foco
El arreglo experimental del sistema montado en el laboratorio se puede observar en la imagen de la Figura 6.
Figura 6. Arreglo experimental de la simulación del relevador de un laparoscopio convencional en laboratorio
Se tomaron medidas para obtener los valores de distancia entre autoimágenes consecutivas, es decir, de autoimagen “positiva” a autoimagen “negativa” (se hizo de esta forma para facilitar el experimento). Primero, se realizaron mediciones sin el relevador, con el propósito de verificar que el haz de luz estuviera colimado correctamente y que el efecto Talbot se cumpliera en el sistema. Los valores obtenidos se muestran en la Tabla 1a. Posteriormente, se obtuvieron los valores al colocar el relevador, los cuales se encuentran en la Tabla 1b.
El error relativo porcentual para cada valor en ambos casos es menor al 2 %. En particular, el error relativo porcentual promedio es de 0.2259 % sin relevador y de 0.3753 % con relevador. Los valores obtenidos están muy cerca del valor teórico esperado, , calculado a partir de la ecuación 2, que es de 15.79 mm. Esto implica una buena exactitud con un sistema de medición que produce una buena precisión.
Tabla 1. Valores entre autoimágenes consecutivas con su respectivo error relativo porcentual para el sistema a) sin relevador y b) con relevador
| Sin relevador | ||
|---|---|---|
| Valores entre autoimágenes consecutivas (mm) |
Error relativo porcentual (%) |
|
| 15.77 | 0.1759 | |
| 15.78 | 0.1126 | |
| 15.83 | 0.2039 | |
| 15.88 | 0.5204 | |
| 15.78 | 0.1126 | |
| 15.77 | 0.1759 | |
| 15.85 | 0.3305 | |
| 15.77 | 0.1759 | |
a)
| Con relevador | ||
|---|---|---|
| Valores entre autoimágenes consecutivas (mm) |
Error relativo porcentual (%) |
|
| 15.82 | 0.1406 | |
| 15.85 | 0.3305 | |
| 15.76 | 0.2392 | |
| 15.77 | 0.1759 | |
| 15.79 | 0.0493 | |
| 15.87 | 0.4571 | |
| 15.83 | 0.2039 | |
| 16.02 | 1.4066 | |
b)
A partir de los valores obtenidos, se realizaron las gráficas que se muestran en la Figura 7. Para la gráfica de la Figura 7a se tomó como el origen la rejilla (n=0), los puntos naranjas son las autoimágenes “positivas” y los verdes las autoimágenes “negativas”. Cada punto tiene su barra de error, determinada por la desviación estándar, y la línea gris representa el valor promedio de los datos.
Por otro lado, en la gráfica de la Figura 7b el punto de origen se colocó en la imagen producida por el sistema 4F (n=0). La representación de los valores en esta gráfica es la misma que la descrita previamente.
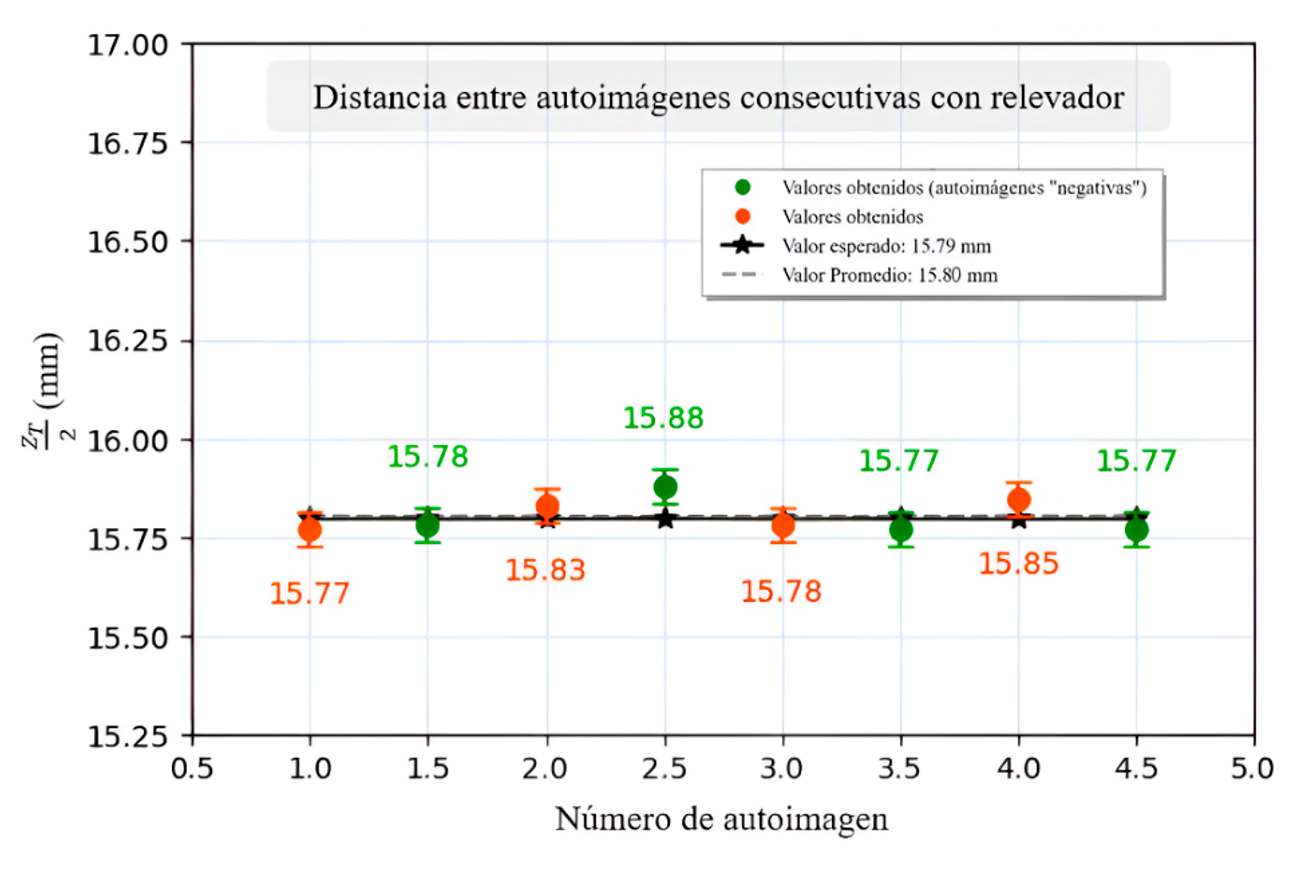
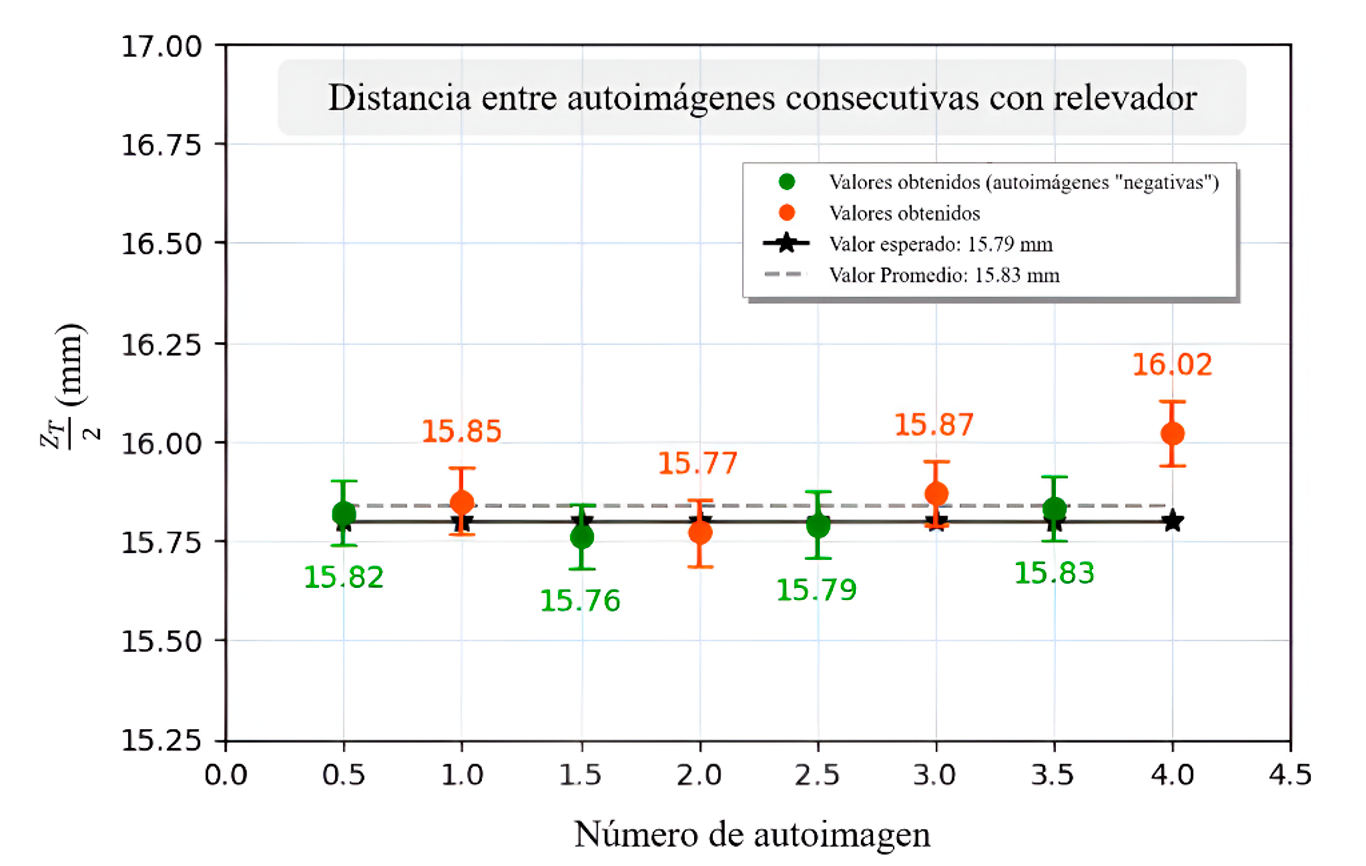
Figura 7. Graficas de las distancias entre autoimágenes consecutivas a) con relevador b) sin relevador
En la Figura 8 se presentan las imágenes de la rejilla. La imagen de la Figura 8a (caso sin relevador) fue tomada a partir de un sistema conformado por una lente, en donde el objeto y la imagen de este se encuentran a una distancia 2F de la lente. Debido a la naturaleza del sistema, la magnificación es 1:1. Por otra parte, para el caso con relevador, se tomó la fotografía de la imagen producida por el sistema 4F (Figura 8b), cuya magnificación también es 1:1. Las dos fotos se tomaron con una cámara CCD.
En el sistema con relevador la imagen de la rejilla se observa como una rotación de ésta. Esto es, como se muestra en la Figura 4, en el sistema de coordenadas x, y, z se encuentra la rejilla en las coordenadas (x, y, z=0). Por otro lado, en el sistema de referencia x’, y’, z’ se encuentra la imagen de la rejilla en las coordenadas (x’, y’, z’=0 (z=4F)). En donde, x’=-x e y=-y, es decir, es una rotación en el plano. Es necesario destacar que las autoimágenes se miden a partir de z’=0. Esta misma rotación sucede en la imagen de la rejilla, de la fotografía tomada con el sistema 2F. Debido a todo lo mencionado, en las fotografías de la Figura 8 se advierte que las imágenes comienzan con una línea transparente, pero originalmente en esa sección de la rejilla comienzan con una línea oscura.
Figura 8. Imagen de la rejilla tomada con a) un sistema 2F b) sistema 4F
En la Figura 10 se presentan seis imágenes autoimágenes producidas por la rejilla tanto en propagación libre como a través del relevador. En la Figura 10a se pueden ver las primeras dos autoimágenes “positivas” junto con la autoimagen “negativa” ubicada entre ellas. Es notable el desplazamiento de medio periodo entre autoimágenes consecutivas, conforme establece el efecto Talbot para rejillas binarias cuadradas [8]. Este comportamiento también se evidencia en la Figura 10b, que son las primeras tres autoimágenes consecutivas del sistema 4F, esto sugiere que el efecto Talbot se conserva al colocar el relevador. Al analizar las imágenes se observa un ligero corrimiento en zonas de la autoimagen “negativa” n=1.5, con respecto a n=1, lo cual puede ser explicado por un error experimental en la obtención de la imagen. Sin embargo, se puede corregir y no afecta la prueba de concepto: Las autoimágenes se forman también a través de un relevador.
Figura 10. Autoimágenes obtenidas con una cámara CCD, a) sin relevador y b) con relevador
Como ya se mencionó, en este experimento, se utilizó λ=633 nm y una rejilla de 10 c/mm, lo que implica un periodo de d=0.1 mm, por lo que, de la ecuación 1, ZT=31.59 mm. Esta distancia es aplicable a algunas partes de la cavidad abdominal y pélvica. Al emplear una rejilla con un periodo menor y la misma longitud de onda, la distancia de Talbot se reduce considerablemente. Por ejemplo, para una rejilla de 50 ciclos por milímetro, o bien, con periodo d=0.02 mm, se obtiene ZT=1.26 mm (ecuación 1), esto permite su aplicación en partes más pequeñas del cuerpo, y así, a otros tipos de endoscopios, como los artroscopios [1].
De acuerdo con los resultados, es posible reproducir autoimágenes a través de un relevador tipo 4F, con las características descritas. En nuestra simulación el error porcentual de la posición entre autoimágenes es menor al 2% y el error porcentual promedio para ambos casos (con y sin relevador) es menor al 1%, lo que comprueba la viabilidad de nuestra propuesta. Es importante destacar que durante el experimento la colimación juega un papel importante, esta puede contribuir en la generación de errores al disminuir o aumentar el tamaño de las autoimágenes.
La formación de autoimágenes a través del relevador es independiente del periodo de la rejilla. Al variar el periodo, se puede variar la distancia entre autoimágenes y, por lo tanto, utilizar la propuesta en diferentes aplicaciones (laparoscopio y/o artroscopios). Esto es, la prueba de concepto es satisfactoria y queda como trabajo a futuro la prueba en un laparoscopio [6].
Obtener PDF