
Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud



Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
La citogenética es la rama de la genética que consiste en el estudio y análisis de los cromosomas, su importancia radica en que a través de su estudio es posible detectar algunas enfermedades congénitas. Cada ser humano tiene 23 pares de cromosomas. Si hay alguna alteración en la forma, el tamaño o el número de estos cromosomas, esto puede indicar una anomalía. Estas alteraciones se pueden detectar mediante el cariotipo, un proceso que identifica cambios en los cromosomas. Para la elaboración de un cariotipo, primero, se obtiene una muestra de tejido vivo (como sangre, líquido amniótico o piel), luego se realiza un cultivo celular para obtener los cromosomas y tomar microfotografías. Con ayuda de un software, las imágenes se procesan en la computadora, se arma el cariotipo y, usando un cariograma, se organizan y clasifican los cromosomas para observar claramente posibles alteraciones. El estudio del cariotipo es de gran utilidad pues desde edades muy tempranas (fetos, recién nacidos o niños pequeños) permite detectar enfermedades cromosómicas como el Síndrome de Down, Síndrome de Turner, entre otras. En este trabajo se utiliza el procesamiento de imágenes como alternativa que apoye a la detección de enfermedades congénitas a través del algoritmo de segmentación basado en los Campos Aleatorios de Markov puesto que se convierte en una herramienta que agiliza la construcción de un cariotipo.
Palabras clave: Campos Aleatorios de Markov, segmentación, cromosomas.
Cytogenetics is a branch of genetics that involves the study and analysis of chromosomes. Its significance stems from the fact that through the examination of that science certain hereditary diseases can be revealed. Each human being possesses twenty-three pairs of chromosomes. If there is any alteration in the shape, size, or number of these chromosomes, it may indicate an anomaly. These alterations are detectable through karyotyping which detects chromosomal alteration. Karyotyping consists, first, a sample of living tissue (such as blood, amniotic fluid, or skin) is obtained, then a cell culture is performed to obtain the chromosomes and take microphotographs. With the software, the images are processed on the computer, the karyotype is assembled and, using a karyogram, the chromosomes are organized and classified to observe any alterations, if present. The study of the karyotype is especially useful because from early ages (fetuses, newborns, or small children) it allows the detection of chromosomal diseases such as Down Syndrome, Turner Syndrome, among others. In this work, image processing is used as an alternative to support the detection of congenital diseases through the segmentation algorithm based on Markov Random Fields, since it becomes a tool that speeds up the construction of a karyotype.
Key words: Markov Random Field, segmentation, chromosome
La citogenética se encarga del estudio, organización y distribución del material genético en las células, así como de la identificación de alteraciones cromosómicas que puedan tener implicaciones en la salud y por ende asociadas a ciertas enfermedades [1].
Este campo de la genética tiene aplicaciones importantes en el diagnóstico y tratamiento de enfermedades genéticas, el análisis forense y la investigación en biología evolutiva y de la reproducción.
El estudio de los cromosomas en humanos es de gran utilidad, pues permite diagnosticar enfermedades genéticas en un feto, un bebé o un niño pequeño, los médicos pueden identificar algunos trastornos genéticos como: síndrome de Down, síndrome de Turner, síndrome de Patau, labio leporino, entre otros.
Existen varias técnicas para el estudio de los cromosomas [2], entre las cuales se destaca:
El presente trabajo se centra en el estudio de la citogenética y la aplicación de técnicas de procesamiento de imágenes para la segmentación y análisis de cromosomas. Se espera que los resultados obtenidos contribuyan al avance y comprensión de este campo de la genética y puedan ser aplicados en el diagnóstico de enfermedades genéticas.
Para el desarrollo del algoritmo se tiene siguiente diagrama (Figura 1). Se introduce una imagen de cromosomas, se realiza un preprocesamiento donde se hace el acondicionamiento de la imagen, posteriormente en el procesamiento se realiza la segmentación de la imagen median el algoritmo K-means que clasificará o agrupará las diferentes tonalidades de grises de la imagen y junto con el algoritmo Campos aleatorios de Markov delimitará los bordes de los cromosomas. Finalmente, en el postprocesamiento, si la imagen de salida es la esperada se detiene el algoritmo sino regresa al preprocesamiento y procede a realizar el proceso de nuevo.
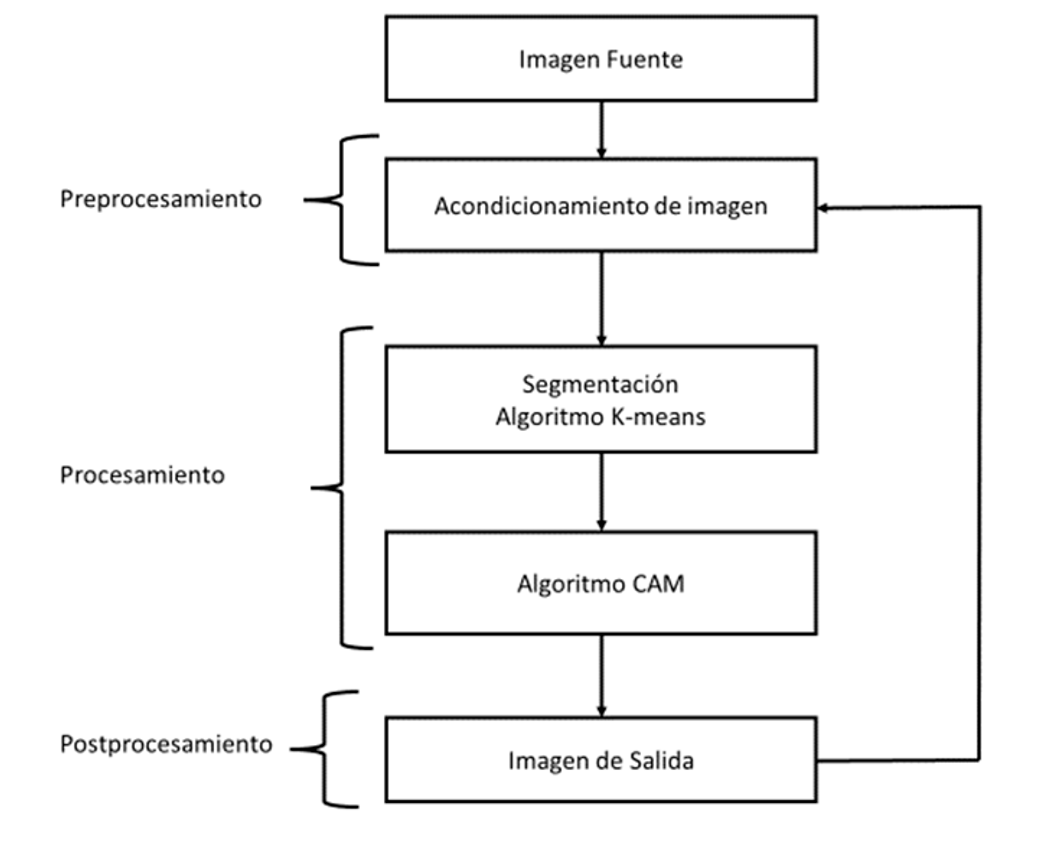
Figura 1. Diagrama de bloques
Hay algunos conceptos que se deben considerar como el sistema de vecindades y cliques, junto con el algoritmo K-means y los Campos Aleatorios de Markov para poder realizar la segmentación de la imagen de los cromosomas.
Sistemas de vecindades y cliques
Una imagen digital se compone de una matriz de m × n píxeles, donde cada píxel está representado por n bits. En una imagen en escala de grises, un píxel representado por n bits puede tener 2^n diferentes tonos de gris. Estos valores de píxel generalmente son enteros, varían desde 0 (píxel negro) hasta 2^(n-1) (píxel blanco). La resolución de una imagen define su calidad, la cual, está determinada por el número total de píxeles en la imagen [3].
La conectividad entre píxeles es comúnmente utilizada para la detección de regiones u objetos en determinada imagen. La vecindad de un píxel se refiere a la relación que tiene dicho píxel con respecto a los píxeles cercanos a su alrededor. Esta relación está definida por el conjunto de estados de una matriz rectangular (imagen), que corresponde a los puntos de una imagen en 2D de tamaño 𝑚 × 𝑛, dado por:
donde i y j representan las coordenadas de un píxel de una imagen m × n. Los estados en 𝑉 están relacionados entre sí a través de un sistema de vecindad, lo que permite identificar y analizar las conexiones entre píxeles para la detección de regiones u objetos en la imagen.
Un sistema de vecindad para 𝑉, se define como:
donde N(i,j) es el conjunto de los estados vecinos de (i,j). En la Figura 2 se muestra la vecindad de un píxel xs de diferente orden. En la Figura 2 (a) se muestra un sistema de vecindad de primer orden, también llamado sistema de 4 vecinos. En (b) es un sistema de segundo orden o un sistema de 8 vecinos. En (c) es un sistema de orden 5, los números s=1,2,…,5 indica el orden del sistema.
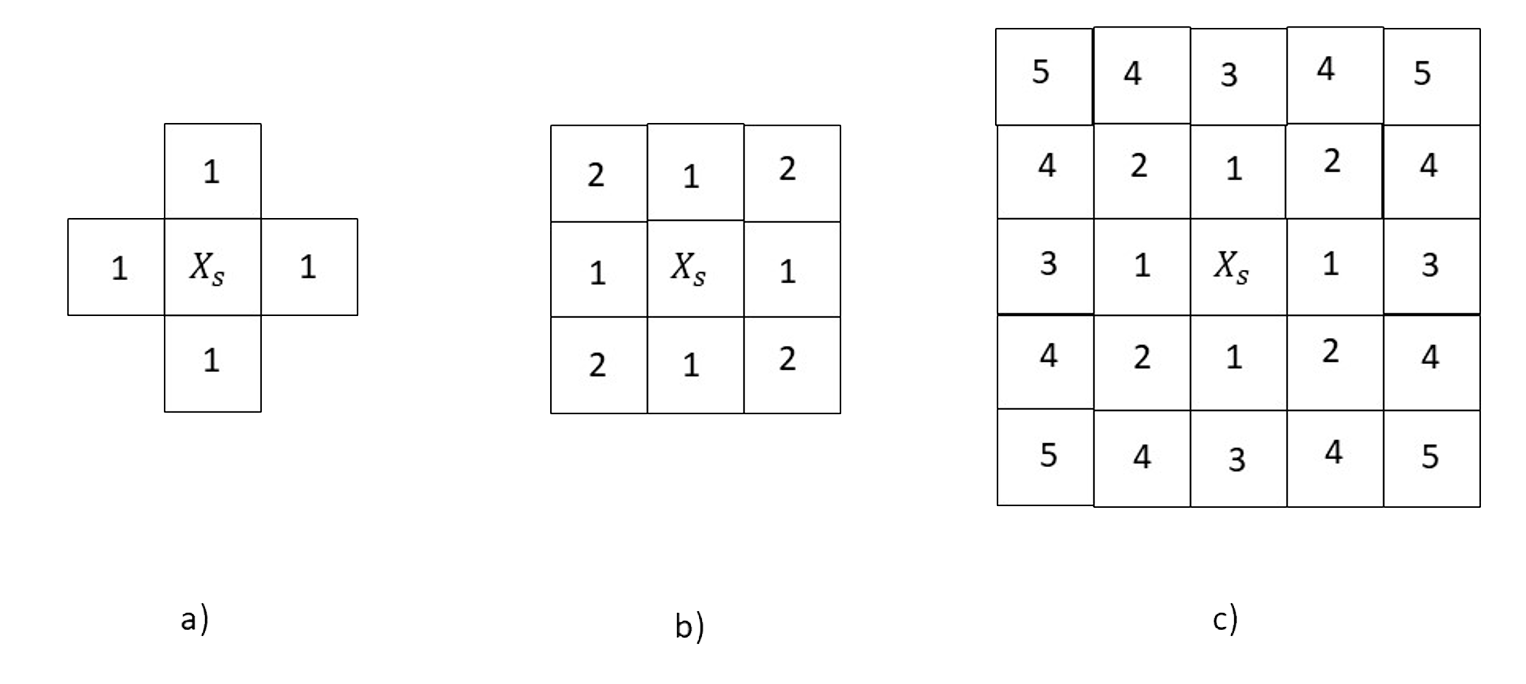
Figura 2. Vecindad
Un clique 𝑐 para (V,N) está definido como un subconjunto de 𝑉, también son conocidos como los píxeles de una imagen que están conectados o relacionados de alguna manera. Los píxeles dentro de un clique que contenga características similares o propiedades comunes que permiten agruparlos. En la Figura 3 se observan los cliques que se pueden formar con los vecinos de xs donde (a) muestra clique de orden 1, (b) y (c) indican un sistema de cloque de orden 2 en vertical, horizontal y diagonal, (d) se muestra el sistema de clique de orden 3 y (e) se muestra un clique de orden 4.
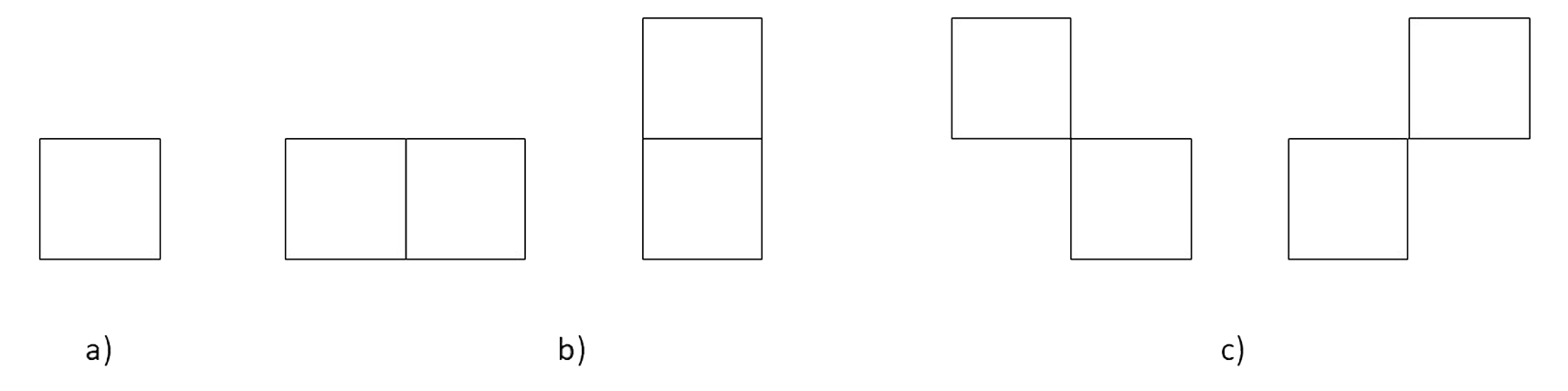
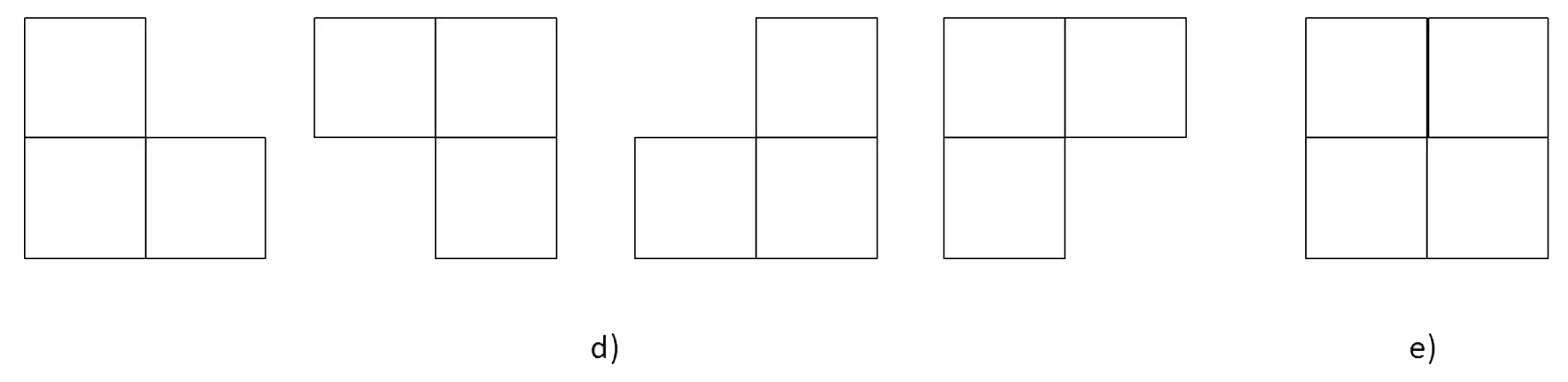
Figura 2. Cliques
K-means
Los campos aleatorios de Markov requieren una herramienta para etiquetar los datos, y una forma efectiva de clasificar estos datos en grupos, es utilizando el algoritmo no supervisado de clustering llamado K-means. Este algoritmo es ampliamente utilizado porque toma decisiones basadas en centroides [4]. El clustering se puede entender de la siguiente manera: dado un conjunto de n objetos y su representación, se pueden formar K grupos basados en sus características, agrupándolos según su similitud mutua.
Dada X = { xi ,i = 1,...,n } donde 𝑋 es un conjunto de objetos que son agrupados en 𝐾 grupos, C = { Ck, k = 1,...,k } . Para lograrlo, este algoritmo consiste en minimizar el error cuadrático entre la media del cluster (el centroide) y los puntos que pertenecen a ese cluster.
Dado 𝜇𝑘 es la media de cada cluster 𝐶𝑘. La función de error cuadrático, que mide la diferencia entre el valor medio 𝜇𝑘 y los puntos contenidos en el cluster 𝐶𝑘, se define como:
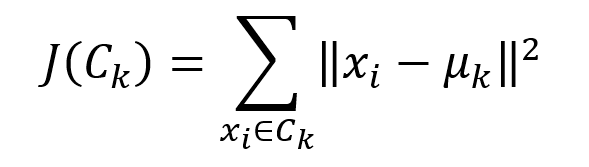
Una vez etiquetado los datos de la imagen, se aplica los campos aleatorios de Markov.
Campos Aleatorios de Markov
Los campos aleatorios proporcionan una manera conveniente y consistente de modelar entidades que dependen del contexto, una de estas entidades son los pixeles. Estos al trabajar con una imagen, son especialmente exitosos en la modelación de problemas de visión tales como la restauración de imágenes, la segmentación, la reconstrucción de superficies, el análisis de texturas, el flujo óptico, la integración visual y la delimitación. Los campos aleatorios de Markov, en el marco de la segmentación de imágenes ayudan a integrar características relevantes, disminuir el ruido y la incertidumbre. Además, estas capacidades contribuyen a mejorar la precisión y la calidad general en la segmentación de imágenes [5,6].
Para llevar a cabo tanto la segmentación como la delimitación de la imagen, se emplea la función de energía que se describe a continuación [7]:

donde 𝛼𝑖, 𝛼𝑗 son los pixeles, 𝑉 el conjunto de pixeles y 𝑁 es el conjunto de estados de vecinos.
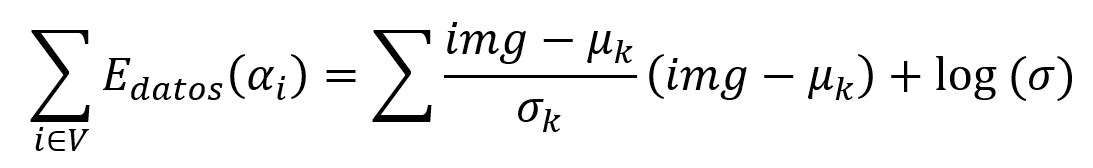
donde 𝜇𝑘 es la media de cada cluster, 𝜎𝑘 la covarianza de cada cluster, 𝑖𝑚𝑔 son los datos de la imagen. Esta función representa la medida de ajuste entre la imagen original y las etiquetas asignadas a cada píxel. Esta función captura la información y características específicas de los datos observados. Y
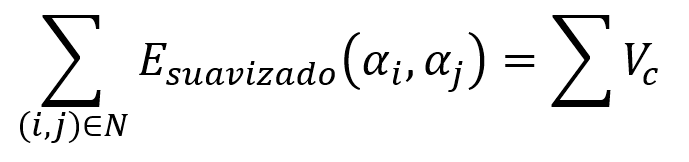
Es la función de energía que modela la regularidad espacial o suavidad deseada en el área segmentada, donde 𝑉𝑐 son los conjuntos de cliques. Esta función penaliza las configuraciones de etiquetas que presentan discontinuidades abruptas entre los píxeles vecinos. El objetivo es obtener una segmentación coherente y suave.
Es posible obtener los resultados de un conjunto de imágenes cromosómicas obtenidas de un laboratorio de genética, las cuales fueron adquiridas siguiendo condiciones de confiabilidad permanentes cabe mencionar que los resultados obtenidos se realizaron en Jupyter Notebook, un entorno de trabajo con lenguaje de programación Python y una computadora con las siguientes características: procesador core i5 de 4 generación (1.6GHz) y 4 GB de RAM. Se presentarán los resultados obtenidos del algoritmo propuesto tras realizar las operaciones con las imágenes de los cromosomas.
En la Figura 4 se ilustra la aplicación de la metodología propuesta a la imagen de cromosomas. En la imagen original (a), se pueden observar los cromosomas. Cuando se emplea un valor de 𝐾 = 2 (b), se destaca el fondo de los cromosomas, mientras que para 𝐾 = 3 (c), comienzan a aparecer las bandas de los cromosomas y se produce una mejora en la imagen. Para 𝐾 = 4 (d), se resaltan los puntos entre las bandas de los cromosomas. A medida que aumentamos 𝐾 = 5 (e), se revelan más detalles, pero también empieza a notarse el ruido en la imagen. Finalmente, para 𝐾 = 6 (f), las líneas que previamente parecían unirse dificultan el análisis completo de la imagen.

Figura 4. Aplicando CAM a cromosomas
En la Figura 5 (a) se presenta la imagen original de un cromosoma, la cual no ha experimentado ninguna modificación. Al aumentar el valor de K, los resultados se observan de la siguiente manera: para 𝐾 = 2 (b), se destaca la diferencia entre el fondo y el objeto de interés, en este caso, el cromosoma. Con 𝐾 = 3 (c), comienzan a ser notables las bandas del cromosoma, y estas se vuelven más definidas en (d) cuando 𝐾 = 4. Al incrementar 𝐾 = 5 (e), las bandas se delimitan aún mejor, revelando más detalles de la estructura cromosómica. Sin embargo, al aumentar 𝐾 = 6 (f), la imagen empieza a mostrar señales de ruido.

Figura 5. Aplicando CAM a cromosoma
Se propuso e implementó una metodología basada en Campos Aleatorios de Markov para abordar la segmentación de cromosomas. Con el fin de lograrlo, se propuso utilizar la segmentación por agrupación apoyándose en el algoritmo K-means. Con esta técnica se obtuvieron resultados satisfactorios que demostraron una mejora en la calidad de las imágenes procesadas. La capacidad de ajustar los parámetros de entrada permite modificar la salida de la imagen, lo que resalta de mejor forma las siluetas y las bandas cromosómicas.
El algoritmo propuesto podría tener un impacto en la salud, en el área de la genética, ya que la segmentación de las diferentes áreas de interés de la imagen hace notar características que no se suelen observarse, también se considera que podría reducir el tiempo a la hora de armar el cariotipo, pero con el uso del algoritmo junto con lo especialista tendría mejoras y podría reducir aún más el tiempo del armado, como se mencionó anteriormente el cariotipo ayuda a detectar enfermedades genéticas, como son alguno síndromes, como el de Patau, Down, Turner, entre otros.