Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud
Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
En la actualidad, los médicos recurren a distintos aparatos para poder generar un diagnóstico por medio de la obtención de imágenes, por lo tanto, es importante el estudio de la mejora de dichas imágenes. El aparato de resonancia magnética (o MRI) es uno de los que proporcionan imágenes de diferentes tejidos por medio de la interacción de los campos magnéticos generados por sus componentes con las moléculas de agua que se encuentran dentro del cuerpo humano. Con este trabajo se obtuvieron los niveles de energía y la función de onda de la molécula de agua al interaccionar con los campos magnéticos generados por dos de las tres componentes principales de un MRI, con la finalidad de que dichos resultados sean de ayuda para la mejora de imágenes médicas.
Palabras claves: Resonancia magnética, MRI, molécula de agua.
Nowadays, doctors use different devices to be able to generate a diagnosis by obtaining images, therefore, the study of the improvement of these images is important. The magnetic resonance imaging (or MRI) device is one of those that provide images of different tissues through the interaction of the magnetic fields generated by its components with the water molecules found inside the human body. With this work, the energy levels and the wave function of the water molecule were obtained when interacting with the magnetic fields generated by two of the three main components of an MRI, with the aim of these results being helpful in improving medical images.
Key words: Magnetic resonance imaging, MRI, water molecule.
Existen variedad de aparatos médicos que proporcionan imágenes de diferentes tejidos por medio de distintos procedimientos, uno de ellos es el resonador magnético, el cual se basa en la interacción de los campos magnéticos generados por algunas de las componentes de dicho aparato con los protones de los hidrógenos de las moléculas de agua que se encuentran dentro del cuerpo humano, ya que la molécula que predomina en él es la molécula de agua, pues en la vida adulta el cuerpo se compone en un 60% de ella [1].
Se obtendrá la función de onda de la molécula de agua considerando el modelo simplificado de ella que se explica en la sección 3.1, para así obtener los niveles de energía correspondientes al estado base y al primer estado excitado de dicho modelo al interaccionar con los campos magnéticos generados por un aparato de resonancia magnética.
3.1 Molécula de agua y su modelo simplificado
La molécula de agua está compuesta por un átomo de oxígeno y dos átomos de hidrógeno unidos por medio de un enlace covalente, esto debido a que el átomo de hidrógeno consta de un solo electrón orbitando alrededor de un núcleo compuesto de un protón y un neutrón, en cambio, el átomo de oxígeno tiene ocho electrones girando alrededor de su núcleo donde seis de ellos se encuentran en la última órbita del átomo faltando justamente dos electrones para que dicha órbita esté completa, por lo tanto, existe una mayor fuerza de atracción de los electrones de los hidrógenos con el átomo de oxígeno, ocasionando así la generación de la molécula de agua.
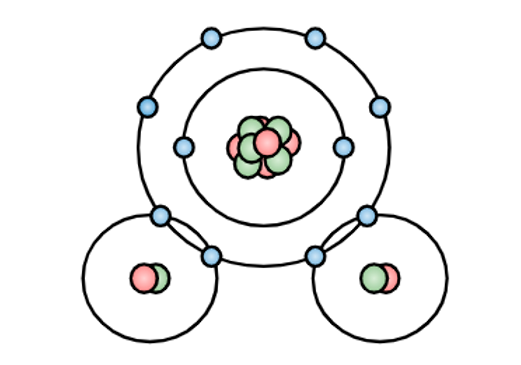
Figura 1. Esquema clásico de la molécula de agua
La investigación se basó en un artículo ya publicado [3]. tomando de él el modelo simplificado de la molécula de agua con el que se trabajó. De la Figura 1 se puede observar que del lado del átomo de oxígeno existe una mayor distribución de carga negativa, en cambio, del lado de los átomos de hidrógeno hay una mayor distribución de carga positiva, por lo tanto, se decidió simplificar el modelo a un sistema de tres cargas puntuales; carga positiva (protón) en lugar de hidrógenos y carga negativa (electrón) en el lugar del oxígeno. Para el nuevo modelo se consideró que no existe una variación en los radios del sistema, por lo tanto, se comporta como un cuerpo rígido con centro de masa en la carga puntual negativa.
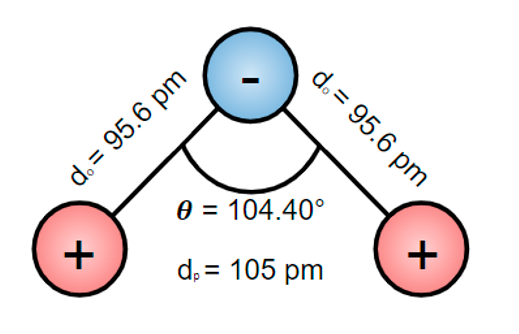
Figura 2. Esquema de modelo simplificado de la molécula de agua
3.2 Resonancia magnética
Los aparatos de resonancia magnética generan campos magnéticos por medio de las siguientes componentes [4]:
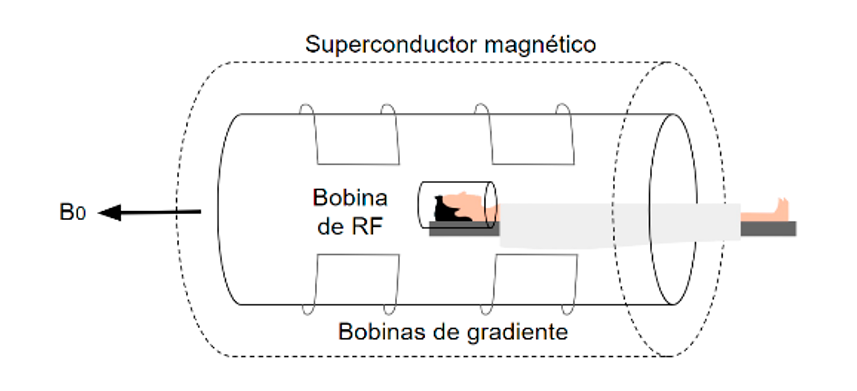
Figura 3. Esquema de las componentes principales de un MRI
El superconductor magnético produce un campo magnético constante en una sola dirección, como se observa en la Figura 3, las bobinas de gradiente generan una variación en dicho campo magnético constante. La expresión del campo magnético generado tanto por el superconductor magnético como por las bobinas de gradiente está dada por la expresión (1).
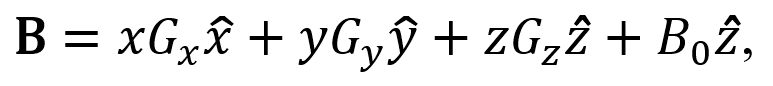
donde xGx, yGy y zGz corresponden a los valores de los gradientes en un punto en específico para las tres coordenadas y B0 es la magnitud del campo magnético constante.
Los protones de los hidrógenos de la molécula de agua preceden a una frecuencia y dirección aleatoria cuando se encuentran fuera de un campo magnético, en cambio, al interaccionar con uno (como el generado por el superconductor magnético de un MRI) comenzarán a preceder a una frecuencia y dirección específica, a dicha frecuencia se le denomina frecuencia de Larmor y está dada por expresión (2).
donde γ es la constante giromagnética de los protones y B el campo magnético externo con el que interaccionan. Los protones al interaccionar con un campo magnético pueden tomar dos posibles direcciones, denominadas paralela y antiparalela, la paralela se encuentra en la dirección del campo magnético y la antiparalela en contra de él, como se puede observar en la Figura 4.
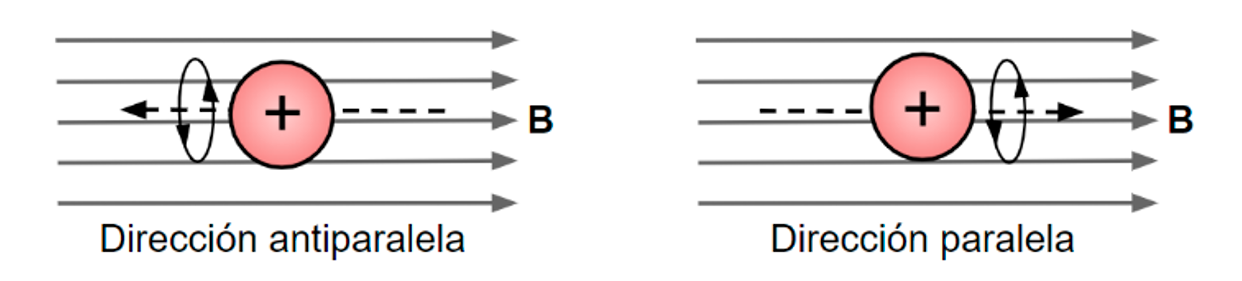
Figura 4. Posibles direcciones de precesión
Los protones que se encuentran en un nivel de menor energía permanecen en la dirección paralela, debido a que es la que está a favor del campo magnético, por lo tanto, es la dirección preferente para las partículas. Sin embargo, lo explicado anteriormente son generalizaciones, puesto que no todos los protones se encuentran precediendo a la misma frecuencia y en alguna de las dos direcciones antes mencionadas con exactitud, existen variaciones derivadas de diferentes fenómenos. Una vez que el cuerpo humano se coloca en el interior de un MRI sucederá lo antes descrito, posteriormente el aparato emitirá pulsos de radiofrecuencia con la frecuencia a la que se encuentran precediendo los protones, esto con la finalidad de que absorban la mayor cantidad de energía posible proveniente de dichos pulsos y así lograr que una vez sean apagados, los protones emitan la energía absorbida para ser procesada y transformada en imágenes.
3.3 Estructura fina
Como se mencionó anteriormente, la frecuencia y dirección con la que preceden todos los protones de las moléculas de agua no es exactamente la misma debido a distintos fenómenos, uno de ellos es el efecto de estructura fina, el cual está dado por las contribuciones del efecto de acoplamiento espín-órbita y el efecto de corrección relativista. El acoplamiento espín-órbita es un fenómeno que ocasiona el cambio en los niveles de energía de las partículas [2] debido a la interacción entre el momento magnético de espín del protón (𝝁p) con el campo magnético generado por el electrón (para este modelo ejemplificado en la Figura 2), dando como resultado el hamiltoniano de la ecuación (3).
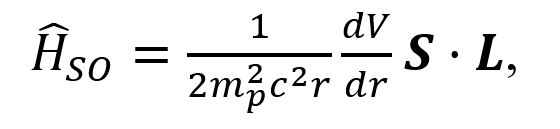
donde mpes la masa del protón, c es la velocidad de la luz, r es la distancia del electrón al protón, V es el potencial de Coulomb generado por el electrón donde los protones se mueven, S y L son los operadores de momento de espín y orbital, respectivamente, cada uno con sus componentes tridimensionales (donde k podrá ser x, y, z).
El efecto de corrección relativista surge debido al movimiento del electrón alrededor del núcleo ocasionando también una variación en los niveles de energía, aunque dicho efecto es pequeño puede ser detectado por técnicas de espectroscopía. La expresión (4) muestra el hamiltoniano de la corrección antes mencionada.
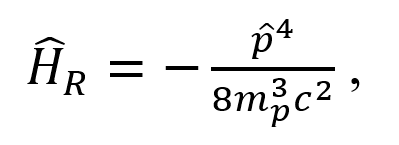
donde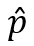 
es el momento lineal del protón. El efecto de estructura fina se encuentra descrito entonces por la ecuación (5) que son la suma de las contribuciones de (3) y (4).
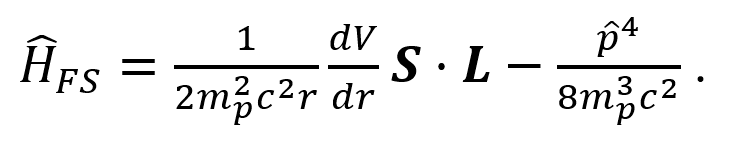
3.4 Efecto Zeeman anómalo
Las variaciones en los niveles de energía debido al efecto Zeeman es a causa de la interacción entre el momento magnético de espín del protón (𝝁p) con un campo magnético externo. El efecto Zeeman no toma en cuenta al espín la partícula a comparación con el efecto Zeeman anómalo donde si se toma en cuenta. La expresión (6) muestra el hamiltoniano del efecto Zeeman anómalo.
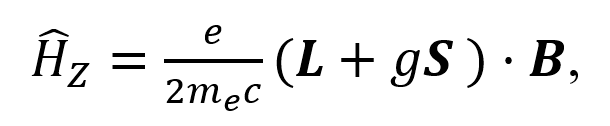
donde B es el campo magnético externo.
4.1 Función de onda
La función de onda para este modelo está dada por la ecuación (7).
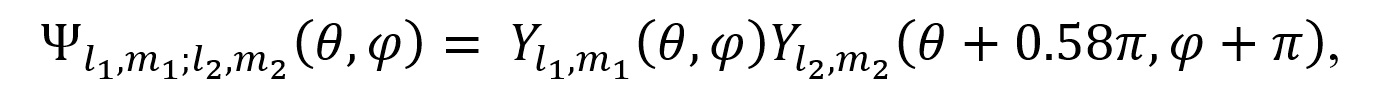
donde las Y representan la parte angular de la solución del átomo de hidrógeno con sus respectivos números cuánticos (l y m), cada Y le corresponde a cada protón. Para obtener la expresión (7) se basó en el artículo antes citado, se agregó la dependencia angular y se graficó dicha función para tres casos que se pueden observar en la Figura 5.
4.2 Obtención de los niveles de energía
Primero se obtuvieron los niveles de energía de la molécula de agua utilizando el modelo antes descrito y la expresión (8) obtenida del mismo artículo.
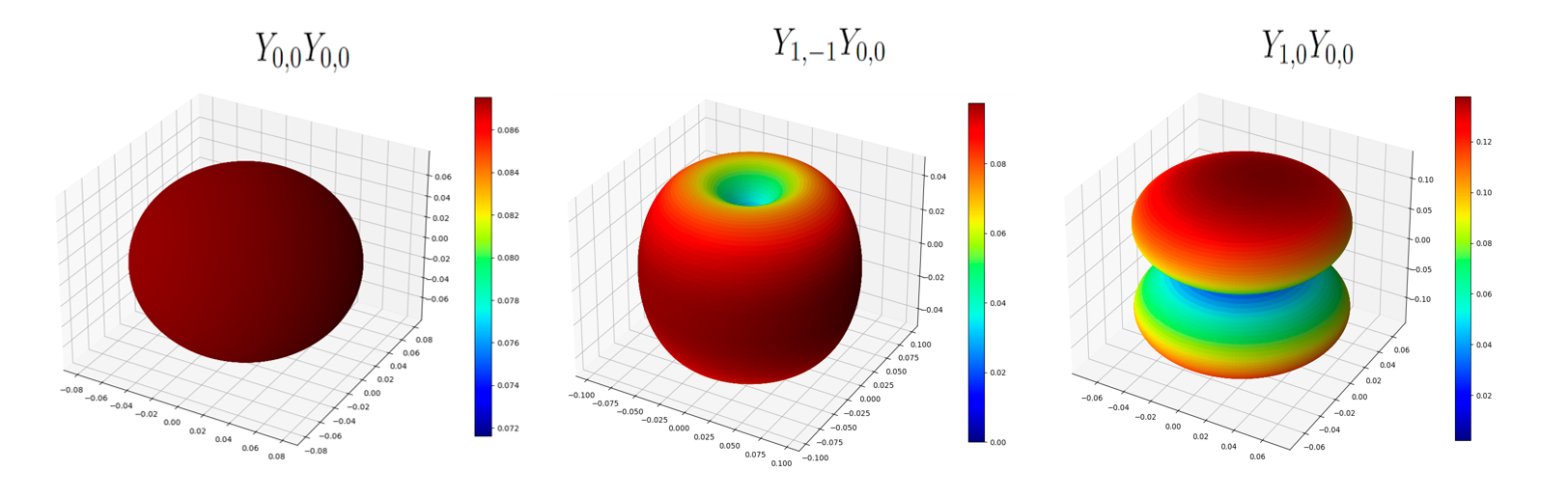
Figura 5. Gráficas de la función de onda para tres casos
donde el subíndice i = 1, 2 representa a cada protón, do es la distancia del electrón al protón (ver Figura 2) y Vi está dada por la ecuación (9).
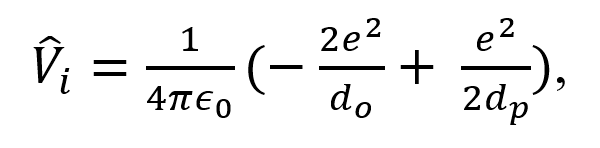
donde dp es la distancia de protón a protón, e es la carga del protón y ϵ0 es la constante de permitividad eléctrica.
Posteriormente se realizó una analogía del efecto de estructura fina para obtener los niveles de energía de la molécula de agua antes de ingresar a un campo magnético, primero se analizó la expresión (3) donde el hamiltoniano depende de la derivada de un potencial y como se mencionó anteriormente, el radio del modelo con el que estamos trabajando no varía, por lo tanto, dicho potencial es constante y la derivada es cero, concluyendo en que el efecto espín-órbita no contribuye en las energías. Por otro lado, se trabajó con la ecuación (4), se obtuvo el valor esperado del hamiltoniano de dicha expresión, para ello primero se despejó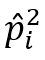 
de la ecuación (10).
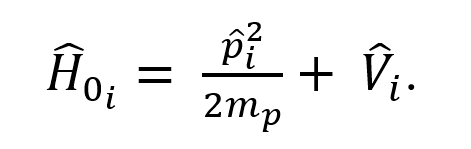
La expresión (10) muestra el hamiltoniano para cada protón al encontrarse sin interaccionar con algún campo magnético. Posteriormente, elevando al cuadrado el despeje obtenido de (10) llegamos a la expresión (11).
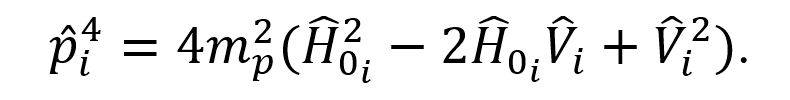
Se sustituyó la ecuación (11) en la (4) y se calculó el valor esperado para así obtener una expresión para las energías.
Se obtuvo después las energías de la molécula de agua al interaccionar con el campo magnético constante generado por el superconductor magnético por medio del efecto Zeeman anómalo, el campo magnético constante se encuentra en la dirección z, por lo tanto, se llegó a la ecuación (13) por medio de la (6).
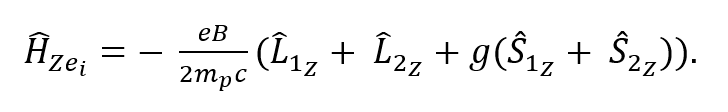
Se calculó el valor esperado de la expresión (13) considerando la ecuación (14).
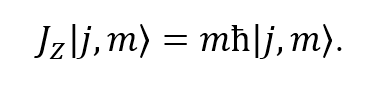
De esa forma se llegó a la expresión (15).
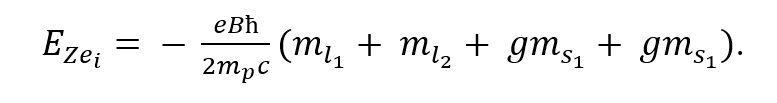
A continuación se calcularon las energías de la molécula al interaccionar ahora con el campo magnético generado por las bobinas de gradiente utilizando igual el efecto Zeeman anómalo, para ello se sustituyó el campo magnético de los gradientes de la ecuación (1) en la ecuación (6) considerando la expresión (16).
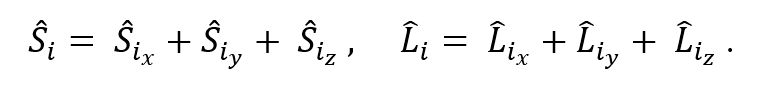
Se obtuvo entonces la expresión (17).
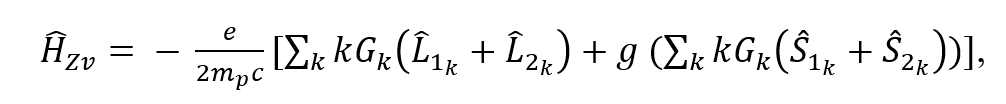
Utilizando las propiedades dadas por (18) y (19) para el momento angular total se obtuvo el valor esperado de (17) dado por la expresión (20).
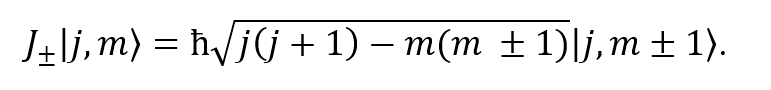
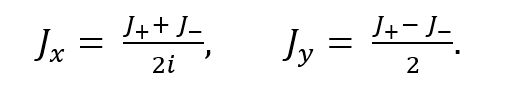
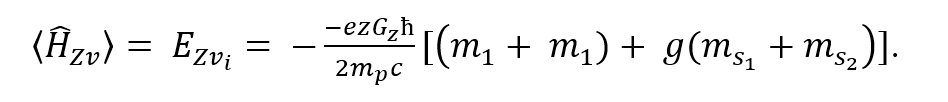
Las energías totales están dadas por la suma de las energías del primer y segundo protón. Por lo tanto, se sustituyeron los valores correspondientes en la ecuación (8), para el estado base se obtuvo que la energía es de -50.71653027 eV y para todos los estados posibles del primer estado excitado se obtuvo que la energía es de -50.71198952 eV. Posteriormente, se sustituyeron los valores correspondientes del estado base y el primer estado excitado en la ecuación (12) para los dos protones y sumando sus respectivas energías se obtuvo que para el estado base, el efecto de estructura fina no ocasiona alguna variación en la energía, pues resultó en cero, pero para el primer estado excitado la energía es de 1.3707x10-6 eV. Consecuentemente se sustituyeron los valores correspondientes a las especificaciones de un MRI Siemens MAGNETOM Skyra 3T MRI Scanner en la ecuación (15) considerando el campo magnético constante y en la ecuación (20) tomando el campo magnético generado por las bobinas de gradiente, esto para el primer y segundo protón. Sumando las energías obtenidas de (15) y (20) una vez sustituidos los valores para el estado base y el primer estado excitado y sumando la energía de 1.3707x10-6 eV solo para el primer estado excitado, se llegó a las energías de la molécula de agua que se muestran en la Tabla 1.
Tabla 1. Energías de la molécula de agua al interaccionar con el campo magnético constante generado por el superconductor magnético y con el generado por las bobinas de gradiente para el primer estado excitado y el estado base
| Estado | (l1, l2; m1, m2; ms1, ms2) | Energía (x10-6eV) |
|---|---|---|
| Base | (0, 0; 0, 0;±,∓) | 0 |
| Primer estado excitado | (1, 0; -1, 0;-,-) | 1.9953 |
| (1, 0; 0, 0;-,-) | 1.9004 | |
| (1, 0; 1, 0;-,-) | 1.8056 | |
| (1, 0; -1, 0; ±,∓) | 1.4655 | |
| (1, 0; 0, 0; ±,∓) | 1.3707 | |
| (1, 0; 1, 0; ±,∓) | 1.2758 | |
| (1, 0; -1, 0;+,+) | 0.9358 | |
| (1, 0; 0, 0;+,+) | 0.8409 | |
| (1, 0; 1, 0;+,+) | 0.7406 |
Por último, se le sumó a la energía del estado base de la Tabla 1 la siguiente energía -50.71653027 eV y a las posibilidades del primer estado excitado de la misma tabla se le sumó -50.71198952 eV, obteniendo así los valores de la Tabla 2.
Tabla 2. Energías de la molécula de agua al interaccionar con el campo magnético generado por las bobinas de gradiente y por el superconductor magnético para el primer estado excitado y el estado base
| Estado | (l1, l2; m1, m2; ms1, ms2) | Energía (eV) |
|---|---|---|
| Base | (0, 0; 0, 0;±,∓) | -50.71653027 |
| Primer estado excitado | (1, 0; -1, 0;-,-) | -50.71198752 |
| (1, 0; 0, 0;-,-) | -50.71198762 | |
| (1, 0; 1, 0;-,-) | -50.71198771 | |
| (1, 0; -1, 0; ±,∓) | -50.71198805 | |
| (1, 0; 0, 0; ±,∓) | -50.71198815 | |
| (1, 0; 1, 0; ±,∓) | -50.71198824 | |
| (1, 0; -1, 0;+,+) | -50.71198858 | |
| (1, 0; 0, 0;+,+) | -50.71198868 | |
| (1, 0; 1, 0;+,+) | -50.71198878 |
De la Tabla 2 podemos observar que existen variaciones en las energías, sin embargo, aún falta obtener las diferencias de energía entre los estados indicados en los resultados, las frecuencias asociadas a esas diferencias son las que requiere el pulso para poder excitar el sistema y realizar esas transiciones, al relajarse el sistema emitirá la energía absorbida, la cual es detectada por las antenas del MRI y procesada para generar las imágenes. Nótese que las transiciones que proporcionarán mayor emisión vienen dadas por dos estados extremos, estos resultan en la mayor diferencia posible, si se tiene una mayor diferencia se tendrá mayor emisión, por lo tanto, mayor señal.
Obtener PDF