Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud
Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
La angiogénesis está estrechamente relacionada con la osteogénesis esto debido a que la contribución de los vasos sanguíneos en las funciones y remodelación ósea ha cobrado recientemente un enorme interés por su potencial terapéutico. Los avances recientes en la comprensión de los vasos sanguíneos y los nichos vasculares en el hueso son de una importancia crítica en la regulación del desarrollo y la fisiología del hueso. Se propuso acoplar los modelos matemáticos de Komarova y Travasso para desarrollar un modelo que combine un diseño de la morfología ósea y su contraparte celular de la vascularización.
Palabras clave: Angiogénesis, osteogénesis, modelos matemáticos.
Angiogenesis is closely related to osteogenesis, as the contribution of blood vessels to bone function and remodeling has recently gained enormous interest for its therapeutic potential. Recent advances in the understanding of blood vessels and vascular niches in bone are of critical importance in regulating bone development and physiology. It was proposed to couple the mathematical models of Komarova and Travasso to develop a model that combines a design of bone morphology and its cellular counterpart of vascularization.
Key words: Angiogenesis, osteogenesis, mathematical models.
Los huesos, los componentes estructurales y mecánicos de nuestro cuerpo, están involucrados en el metabolismo de todo el cuerpo, las funciones cerebrales, la homeostasis mineral y la generación de células sanguíneas [1,2]. Estos son tejidos altamente vascularizados, metabólicamente activos que tienen una extensa red de vasos sanguíneos excepto en las regiones cartilaginosas [1,3]. Los vasos sanguíneos no son solo conductos de transporte; las células endoteliales (CE: las unidades constructoras de los túbulos de los vasos sanguíneos), interactúan estrechamente con las células tisulares para regular su fisiología y funciones como hematopoyesis y osteogénesis [4].
El proceso de formación ósea comienza en el útero y continúa hasta la vida adulta con el fin de reparar fracturas y remodelar los huesos en función de las demandas fisiológicas. Existen dos mecanismos distintos de osificación, endocondral e intramembranosa [5], los cuales median la formación ósea en mamíferos. Durante ambos mecanismos, el factor de crecimiento endotelial vascular (VEGF) atrae a las CE para vascularizar el tejido óseo. La vascularización coincide con la aparición de células óseas y hematopoyéticas [4,6]. También se muestra que la vasculatura influye en la morfogénesis del hueso en desarrollo [7].
La angiogénesis, proceso de formación de nuevos vasos sanguíneos a partir de un vaso existente, también juega un papel crucial en la regulación del desarrollo óseo, ya que está acoplada con la osteogénesis (formación ósea) y la condrogénesis (formación de cartílago) [4]. Varias pruebas indican un modo único de crecimiento de los vasos sanguíneos en el hueso en comparación con otros tejidos, que experimentan modos de angiogénesis por brotación o intususcepción. La angiogénesis por brotación se observa generalmente involucrando ‘células de la punta’ endoteliales en el frente principal de los nuevos brotes de vasos, que exhiben largas extensiones o filopodios en la dirección de factores angiogénicos como VEGF. Las ‘células del tallo’ siguen y proliferan para alargar el brote [4]. Esto se ha observado en el cáncer, así como en el embrión, incluso durante la formación del cerebro. La angiogénesis intususceptiva es la división de los vasos existentes por columnas de células y se observa durante el desarrollo de los pulmones y el corazón [8].
Es por ello que es de gran importancia simular detalladamente estos procesos, debido a que permitirian conocer las diferentes etapas y procesos en el desarrollo del cáncer de hueso. El modelado matemático de sistemas biológicos es una base para poder realizar este tipo de simulaciones. Este tiene su origen en el trabajo pionero de científicos como Alfred Lotka y Vito Volterra, quienes desarrollaron modelos para entender las dinámicas de poblaciones depredador-presa a principios del siglo XX. Posteriormente, el enfoque se amplió para abarcar una amplia gama de sistemas biológicos, con el avance de la computación en la segunda mitad del siglo XX, se pudieron realizar simulaciones más complejas y detalladas, permitiendo la verificación de datos experimentales y la realización de análisis más precisos. Hoy en día, el modelado matemático es una herramienta fundamental en biología de sistemas, biomedicina y ecología, facilitando la comprensión y la predicción del comportamiento de sistemas biológicos complejos.
El remodelado óseo se produce en lugares espacial y temporalmente diferenciados del esqueleto e implica la reabsorción del tejido mineralizado existente por parte de los osteoclastos, seguida de la formación de hueso nuevo por parte de los osteoblastos [9,10]. El modelado matemático de la remodelación ósea se ha centrado en varios aspectos de este proceso y se lleva a cabo por dos vías, la primera es por medio de modelos teóricos que permiten explicar la dinámica espacio-temporal, obteniendo patrones con microestructura análoga al tejido óseo a partir de estos; la segunda es a partir de investigaciones experimentales, donde utilizando nuevas tecnologías de procesamiento de materiales se permite la creación de matrices poliméricas con mejores propiedades de biocompatibilidad [9,10]. Los modelos matemáticos de la angiogénesis han sido fundamentalmente de dos tipos: descripciones microscópicas que explican la dinámica celular y las descripciones de grano grueso basadas en ecuaciones de difusión [11]. El estudio del comportamiento emergente de una red vascular recién formada necesita un enfoque unificado. Por lo tanto, la morfología final de la red vascular depende tanto de los fenómenos que ocurren a nivel celular (por ejemplo, la activación y el brote posterior de nuevas ramas), como de los movimientos colectivos a escala macroscópica de las células debido a la proliferación de células endoteliales y las propiedades del tejido [12].
En este trabajo presentamos un modelo que combina el diseño de la morfología ósea con su contraparte celular de la vascularización, acoplando los modelos matemáticos de Komarova [9] y Travasso [13]. El primer modelo permite calcular la dinámica celular de las interacciones autocrinas y paracrinas entre osteoblastos y osteoclastos, utilizando un término de difusión para describir el proceso de remodelación ósea desde una perspectiva biológica. El segundo modelo representa la formación vascular, permitiendo comparar la estructura ósea con y sin vascularización para descubrir cómo se ve afectada la morfología de los huesos largos.
El modelo planteado por Svetlana V. Komarova [10], describe la dinámica de la población de células óseas, con el número de osteoclastos y osteoblastos denotado por C y B, respectivamente en una sola unidad multicelular básica (BMU). En este modelo, tanto los osteoclastos como los osteoblastos pueden producir efectores locales capaces de activarse o inhibirse a sí mismos o a otro tipo celular.
Por otro lado, el modelo planteado por Travasso [13] establece que la dinámica de la interfaz entre los capilares recién formados (ϕ>0) y los factores angiogénicos (T>0) son tratados con un formalismo de un modelo tipo de campo de fase (ϕ) [14]. La activación del fenotipo de células de la punta en las células endoteliales es el resultado de su respuesta al medio ambiente a través de procesos internos de regulación genética. Este complejo proceso se implementa en el modelo a través de un componente basado en agentes. El modelo de campo de fase rastrea la posición de los capilares y los parámetros como son: tasa de proliferación, velocidad celular y constantes de difusión, estas se pueden relacionar directamente con cantidades medidas experimentalmente.
El modelo de remodelación ósea considera la región del hueso hasta el nivel celular, con influencia de factores locales, las células proliferativas y no activadas se describen mediante un parámetro de orden que es igual a -1 fuera del capilar y +1 dentro de ella. Suponemos que la dinámica de las células endoteliales del tallo es el resultado del equilibrio entre el término de proliferación celular, regulado por la concentración de factor angiogénico, y el término que describe la dinámica del vaso. También suponemos que existe un límite bien definido entre la pared del vaso y el tejido. Por lo tanto, tenemos:
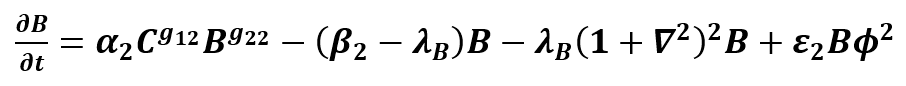
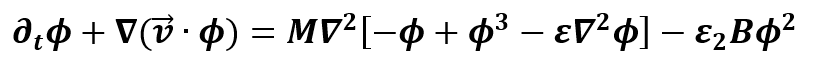
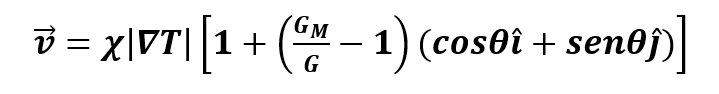
donde C y B son el número de osteoclastos y osteoblastos; α_i y β_i son las actividades de producción y eliminación de células; los parámetros g_ij representan la eficacia neta de los factores autocrinos o paracrinos derivados de los osteoclastos. Una propiedad destacable es que las células son capaces de moverse de forma independiente a través de la matriz extracelular. Este movimiento celular puede definirse por la interacción de las células con sus vecinos más cercanos. Teórica y experimentalmente, la difusión puede ser reemplazada por la combinación de los mecanismos subyacentes con interacciones espaciales de largo y corto alcance, estos comportamientos biológicos se consideran matemáticamente en los términos ΛC (1+∇2 )2 C, λB (1+∇2 )2 B, con λB, ΛC términos constantes. Z representa la masa ósea de acuerdo con una tasa de recambio óseo, con las constantes k1 y k2 siendo la tasa de reabsorción y formación ósea respectivamente, por célula osteoprogenitora al día [9]. Los valores de ϕ corresponden a zonas de proliferación de células endoteliales que dan lugar al ensanchamiento del capilar, M es el coeficiente de movilidad de las células endoteliales,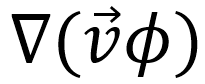 
es la tasa de proliferación de las células endoteliales, χ es la respuesta quimiotáctica de las células endoteliales, |∇T| representa al factor angiogénico y además, ε1,2 Bϕ2es el termino de acoplamiento que muestra la interacción de células osteoblásticas en las zonas de proliferación de células endoteliales.
La primera ecuación del modelo extendido representa el comportamiento dinámico con evolución temporal en la población de osteoclastos que depende de ellos mismos y también de la población de osteoblastos modulados por un conjunto de factores locales. La segunda ecuación del modelo extendido representa la dinámica en la población de osteoblastos que depende del tiempo y también de la población de osteoclastos modulados por un conjunto de factores locales. La tercera ecuación del modelo extendido describe el comportamiento dinámico espaciotemporal de la densidad de masa ósea de acuerdo con una tasa de recambio del tejido, que es dependiente de la población activa de osteoclastos y osteoblastos con la condición inicial Z0 = Z0. La cuarta ecuación describe la dinámica de la interfaz capilar – tejido y la proliferación de células del tallo. Por último, la quinta ecuación representa la velocidad de las células endoteliales de punta. Para los parámetros iniciales del modelo, se utilizó como estimación inicial lo ya propuesto por Komarova, que son datos experimentales obtenidos del análisis histomorfométrico de secciones óseas, dicha información se encuentra resumida en la Tabla 1.
Tabla 1. Valores de los parámetros de control para la obtención de la solución numérica
| Parámetro | β1 | β2 | α1 | α2 | k1 | k2 | g11 | g22 |
| Valor | 0.2 día-1 | 0.02 día-1 | 3 día-1 | 4 día-1 | 0.24 día-1 | 0.0017 día-1 | -0.5 | 0 |
| Parámetro | g21 | g12 | M | ε1 | ε2 | GM | G | T |
| Valor | -0.5 | 1.0 | 1.0 | 1.0 | 0 | 0.03 | 10 | 0.061 |
Se llevó a cabo la simulación del modelo acoplado Komarova - Travasso utilizando el método numérico de Euler mejorado y diferencia finita en un arreglo cuadrado compuesto por una malla de 128×128 a 300,000 iteraciones en un paso de tiempo dt=1×10-7. La solución numérica del modelo se obtuvo mediante la simulación computacional implementada en el software Phyton 3.11 y sus librerías (math, numpy, pylab, tkinter,) y la programación de las Ecs (1) a (5). La Figura 1 muestra los resultados de los patrones obtenidos de la solución numérica del crecimiento de la red capilar (zonas naranjas) respecto a los cambios en la distribución de los osteoblastos (zonas amarillas).
En la Figura 1, A-B) que muestran una red vascular en función de las células osteoblásticas, se observa cómo las interacciones entre los vasos sanguíneos y las células óseas juegan un papel crucial en la regulación de la señalización celular. Se observa como partiendo de un único vaso (en la esquina superior izquierda de la Figura 1A en rojo) cerca de un grupo de células hipóxicas (regiones azules en la Figura 1A) que producen factor angiogénico, emerge una red capilar. A medida que las células de la punta se activan, migran hacia el gradiente de factor angiogénico de manera radial, mostrando una estructura ramificada donde los capilares pequeños brotan de los grandes. En la Figura 1B) se observa como las células osteoblásticas (regiones amarillas) siguen una ruta radial en paralelo a la red vascular.
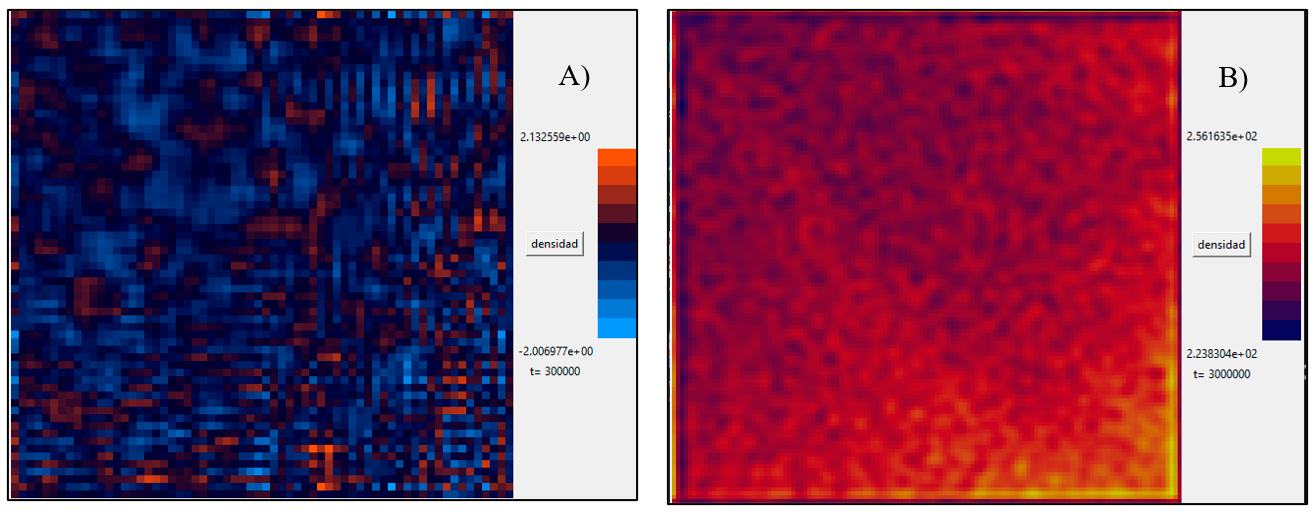
Figura 1. Resultados numéricos obtenidos, A) Crecimiento de la red vascular, B) Densidad poblacional de osteoblastos. Para 300,000 iteraciones
Las células osteoblásticas, encargadas de la formación del hueso, no solo dependen del suministro de nutrientes y oxígeno proporcionado por la red capilar, sino que también influyen en la dirección y la intensidad de las rutas de señalización que guían su diferenciación y actividad. La proximidad de estas células a los vasos sanguíneos parece ser un factor determinante en la modulación de las señales bioquímicas que controlan procesos como la mineralización ósea y la remodelación del tejido, lo que subraya la importancia de la angiogénesis en la homeostasis ósea y su potencial como objetivo terapéutico en enfermedades relacionadas con el hueso.
El modelo presentado reproduce patrones de redes vasculares recién formadas (longitud corta). Este enfoque tiene la ventaja de producir redes vasculares, in – silico que pueden inspeccionarse desde un punto de vista morfológico. El modelo simula los principales mecanismos responsables de la formación de patrones vasculares. La red resultante es únicamente una función de las propiedades de difusión de corto y largo alcance, la quimiotaxis modulada por la cantidad del factor angiogénico y su velocidad, así como de la tasa de crecimiento vascular que determina la dinámica endócrina y paracrina del proceso de remodelación ósea.
Los cambios en la contribución de un tipo particular de célula en el microambiente óseo darían como resultado alteraciones funcionales específicas de la morfología del hueso. El papel central que desempeñan los vasos sanguíneos en la fisiología ósea, indica la necesidad urgente de estudiar la heterogeneidad vascular para comprender la existencia de múltiples microambientes dentro del hueso, lo cual es el motivo de estudios futuros.
Obtener PDF