Actas del Congreso Nacional de
Tecnología Aplicada a Ciencias
de la Salud
Actas del Congreso Nacional de Tecnología Aplicada a Ciencias de la Salud Vol. 6, 2024
Este trabajo se centra en el desarrollo de un módulo de análisis wavelet para integrarlo y fortalecer la interfaz gráfica de usuario “FIMALOF” que procesa señales electroencefalográficas, desarrollada en MATLAB. Las ventajas que presenta esta interfaz es que el usuario no requiere de conocimientos de programación, sus módulos son intuitivos y de fácil manejo, y contribuye en la integración de un módulo que proporcione análisis wavelet con herramientas accesibles para el procesamiento de señales. En dicho módulo, se implementaron diferentes wavelets madre, como Daubechies, Meyer, Symlets y Coiflet. Se presentan ejemplos de la acción del filtrado a través de las wavelets incluidas en el módulo para una señal electroencefalográfica sintética contaminada con un artefacto muscular. Para determinar cuál wavelet es las más eficiente se utilizó el coeficiente de correlación de Pearson, con el que se determinó que la wavelet Coiflet 4 con un nivel de descomposición de 2, ofreció el mejor resultado.
Palabras claves: Wavelet, electroencefalograma, interfaz
This work focuses on developing a wavelet analysis module to integrate and strengthen the graphical user interface "FIMALOF" that processes electroencephalographic signals. This interface is developed in MATLAB. The advantages of this interface are that the user does not require programming knowledge, its modules are intuitive and easy to use, and it contributes to integrating a module that provides wavelet analysis with accessible tools for signal processing. This module implemented different mother wavelets, such as Daubechies, Meyer, Symlets, and Coiflet. The work also presents examples of the filtering action through the module's wavelets for a synthetic electroencephalographic signal contaminated with a muscular artifact. The Pearson correlation coefficient is used as a criterion to determine which wavelet is the most efficient. After the analysis, the Coiflet 4 wavelet with a decomposition level 2 gave the best result.
Key words: Wavelet, electroencephalogram, interface
El cerebro humano, con aproximadamente 100 000 millones de neuronas1, es de gran interés para especialistas de diferentes áreas. La importancia de comprender el funcionamiento del cerebro se vuelve crucial en el contexto de la salud, dado que, según la Organización Mundial de la Salud (OMS) en 2019, 1 de cada 8 personas presentaban un trastorno neurológico2; esta cifra continúa en aumento debido a diversas alteraciones, entre ellas las asociadas con COVID-193. Por esta razón, el desarrollo de herramientas para el análisis de señales de electroencefalográficas (EEG) que permitan profundizar en el estudio del cerebro se vuelve fundamental en el campo de la neurociencia. Existen interfaces gráficas de usuarios (graphic user interface, GUI, por sus siglas en inglés) para el procesamiento de señales de EEG, tales como: BrainVision Analyzer, Compumedics Neuroscan Curry, EEGLAB, G.TEC Guger Technologies, NeuroPype, entre otras. Aunque cada una contribuye al análisis de señales, suelen presentar limitaciones de accesibilidad debido a costos de licencias, problemas de funcionalidad como en EEGLAB con los formatos de entrada4, dificultad de manejo de la interfaz o software debido a su alta complejidad, requerimientos de conocimientos avanzados en programación, además de no mostrar de forma específica las herramientas que ofrecen. Por ejemplo, BrainVision Analyzer5 y CURRY6 mencionan que incluyen análisis wavelet, pero no se muestra qué tipo de wavelets se pueden utilizar.
Como alternativa para contribuir en esta dirección, se está desarrollando una GUI denominada FIMALOF (Filtrado de señales, Mapeo y Localización de Fuentes)4,7. Esta interfaz tiene como objetivo ser una herramienta accesible e intuitiva para el análisis de señales EEG, presentada en español e inglés. La interfaz permite un análisis completo de las señales gracias a sus diferentes módulos. Por ejemplo, el módulo de Análisis de Componentes Independientes (ICA) que divide la señal en múltiples componentes para distinguir entre la información fisiológica y los artefactos. Por otro lado, la Descomposición Empírica de Modos (EMD) elimina artefactos en las frecuencias más altas o bajas de las señales EEG. FIMALOF admite cargar el EEG en diferentes formatos, como .edf, .cnt y .csv, y aplicar filtros digitales (pasa altas, pasa bajas, pasa banda y banda eliminada) en diferentes aproximaciones (Butterwort, Chebyshev, Chebyshev Inverso, Elíptico). Además del filtrado, la interfaz provee un módulo para generar señales sintéticas por medio de una fuente creada a partir de un modelo matemático, como se describe en7, permitiendo a los usuarios controlar las condiciones y parámetros para generar señales que representen diferentes tipos de actividad cerebral y poder evaluar la eficacia de las herramientas de procesamiento en una amplia gama de representaciones.
Debido a la naturaleza estocástica y no estacionaria del EEG8–10, se pretende incluir un módulo de análisis Wavelet para fortalecer la interfaz. Este módulo permitirá utilizar diferentes wavelets madre, como Daubechies, Symlets, Meyer, Haar, entre otras, lo que permitirá encontrar la wavelet madre más adecuada para el procesamiento de una señal específica.
2.1 Clasificación de las señales
Una señal se define como una magnitud física que transmite cierto tipo de información. Las señales se pueden clasificar en dos grupos11,12:
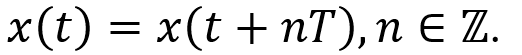
El método más usual para el análisis espectral del EEG es la transformada de Fourier (TF). Esta técnica asume que las señales están compuestas por oscilaciones sinusoidales superpuestas, de amplitudes constantes y periodos en un rango de frecuencia preestablecido. Sin embargo, esta suposición decrementa la confiabilidad del método, dado que el EEG representa la interacción entre redes neuronales, que no es necesariamente lineal13. Por ello, el EEG se considera de naturaleza estocástica no estacionaria8–10, por lo que pueden aprovecharse diferentes técnicas, métodos matemáticos y numéricos para sus análisis.
2.2 Wavelets
Las wavelets son una forma de onda de duración limitada, tienden a ser irregulares y asimétricas14 en comparación a las ondas sinusoidales, las cuales son la base del análisis de Fourier. De manera similar al análisis de Fourier, el análisis de wavelets consiste en descomponer una señal en versiones desplazadas y escaladas de la wavelet original o wavelet madre. Matemáticamente, una wavelet es una función ψ(t) de cuadrado integrable que satisface la condición de admisibilidad11:
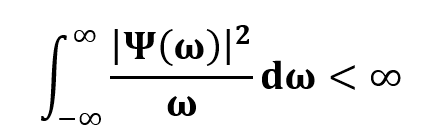
donde Ψ(ω) es la TF (expresión en el dominio de la frecuencia) de la función wavelet ψ(t) (en el dominio del tiempo). Al expandir y desplazar la wavelet, es posible generar una serie de ondas, conocidas como familia wavelet. Se puede obtener mediante:
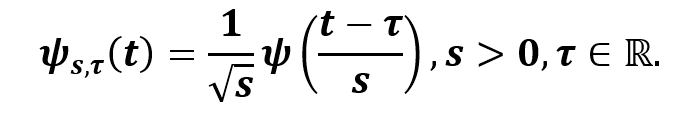
En la figura 1 se ilustra la relación entre ψ(t) y ψs,τ (t), la cual se nombra familia wavelets. Por su parte, la descomposición de una señal para su análisis mediante la obtención de una familia de wavelets escalados y trasladados es denominada transformada wavelet (TW). La Transformada Wavelet Continua (TWC) se define como10:
Para obtener la Transformada Wavelet Discreta (TWD) se discretiza la escala y la traslación mediante s=a-j y τ=2-j k, se tiene que la familia wavelet se puede expresar mediante:
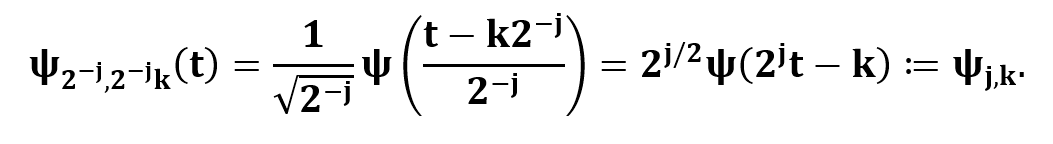
La TWD se define como:
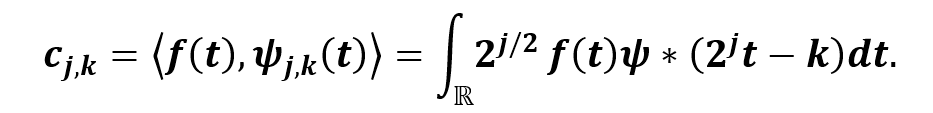
a reconstrucción de la señal a partir de los coeficientes de la TWD se define como:
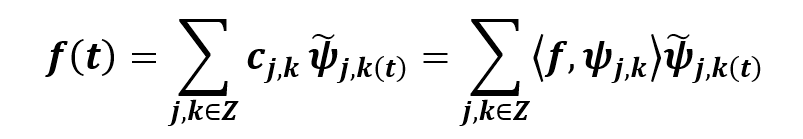
en donde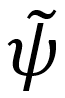 
se define como una wavelet de síntesis o wavelet dual que satisfaga la reconstrucción de la señal.
En la figura 1 se representa como la transformada wavelet actúa sobre una señal x(t), a partir de una wavelet madre, en donde se puede apreciar la variación de los parámetros s y τ, dando como resultado un análisis multiresolución de la señal, así como una localización en tiempo y frecuencia, siendo estas razones por las que se considera que la TW es más eficiente que la TF15–17.
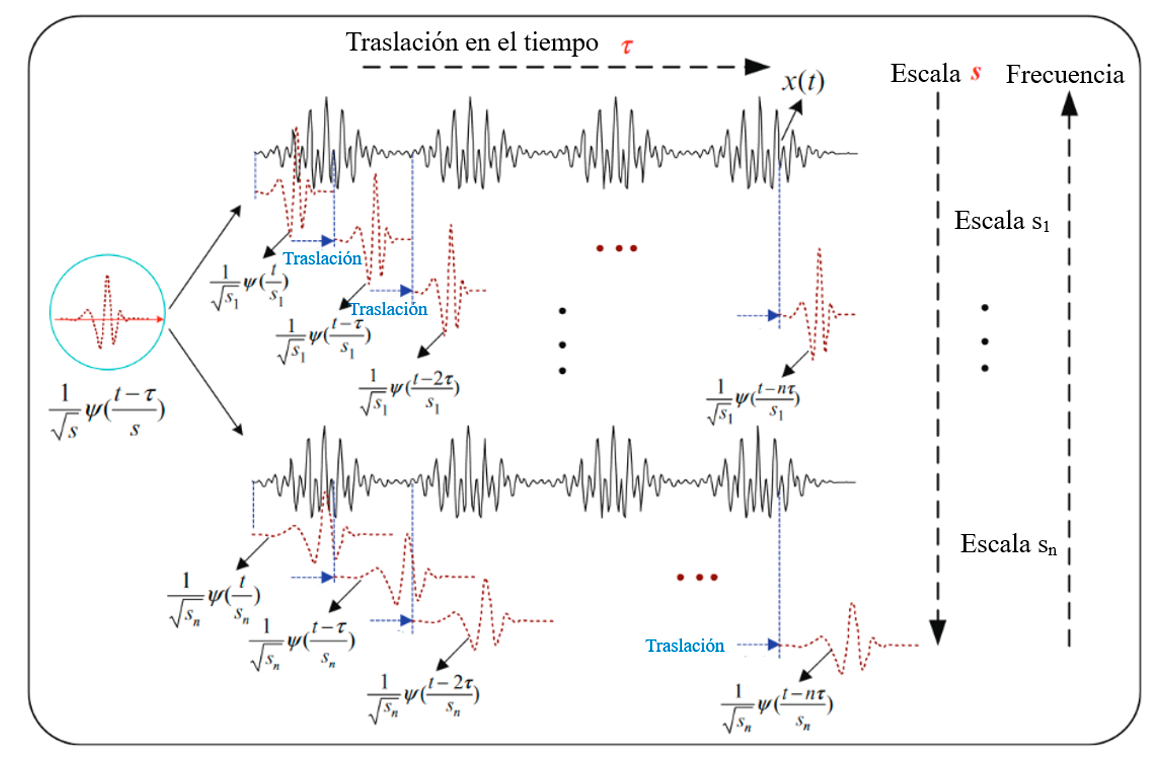
Figura 1. Acción de la transformada wavelet en una señal, retomado de11
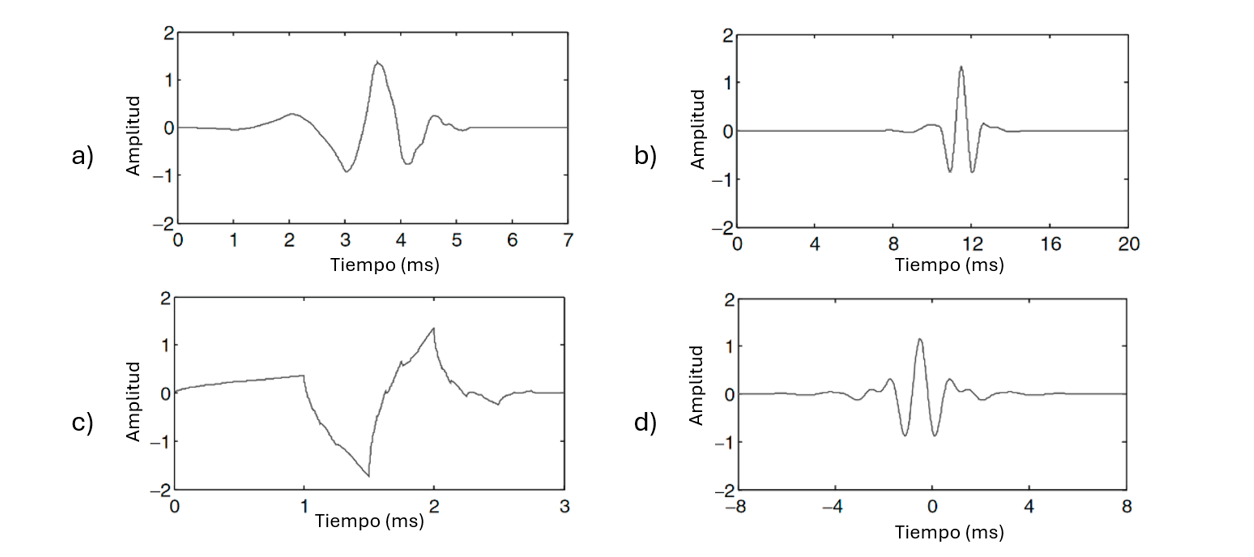
Figura 2. Tipos de wavelets: a) Daubechies (db4), b) Coiflet 4 (coi4), c) Morlet, d) Meyer
Existen diferentes tipos de wavelets, tanto para un análisis con la TWC como para la TWD, algunas de ellas se muestran en la figura 2.
FIMALOF es una interfaz gráfica de usuario desarrollada en MATLAB para el análisis de señales de electroencefalografía4. Su objetivo principal es proporcionar una herramienta accesible e intuitiva que permita a usuarios con diferentes niveles de experiencia aplicar técnicas avanzadas de análisis sin necesidad de conocimientos de programación. El diseño amigable incluye instrucciones claras y mensajes de ayuda, ofrece diversos módulos para el procesamiento de señales EEG, como filtros digitales, ICA, ICA con filtro pasa bajas (ICA-LPF) y EMD, así como un módulo de generación de señales sintéticas que facilita la validación de los diferentes módulos de la interfaz. En este trabajo, se incorpora a la interfaz un módulo de análisis wavelet que permite realizar análisis tiempo-frecuencia de las señales EEG mediante la TWD y la TWC. El usuario puede seleccionar entre diferentes wavelets madre, como Daubechies, Symlets, Meyer y Haar, para encontrar la más eficiente o adecuada para su análisis. Dentro de este módulo, el usuario también puede ajustar el nivel de descomposición y los umbrales para el filtrado de la señal.
Esta interfaz destaca por su accesibilidad, facilitando el análisis de señales EEG a usuarios sin experiencia en programación, integra diversas técnicas de procesamiento, brindando flexibilidad al permitir ajustar los parámetros de análisis y combinar diferentes técnicas. La generación de señales sintéticas ofrece un entorno controlado para la validación y la experimentación. Puede ser utilizada en aplicaciones de investigación en neurociencias, así como para la enseñanza del procesamiento de señales.
El módulo para el análisis de señales con wavelets se ha implementado en la interfaz, en la figura 3 se muestra el menú de opciones que ofrece FIMALOF.
Figura 3. Menú de opciones de interfaz gráfica de usuario FIMALOF con integración de módulo wavelet.
Para ilustrar el funcionamiento del módulo se realizó el procesamiento de una señal sintética contaminada con un artefacto muscular. En la figura 4 se presenta un diagrama a bloques de la metodología, así como las wavelets utilizadas, a saber: Daubechies, Symlet, Meyer y Coiflet.
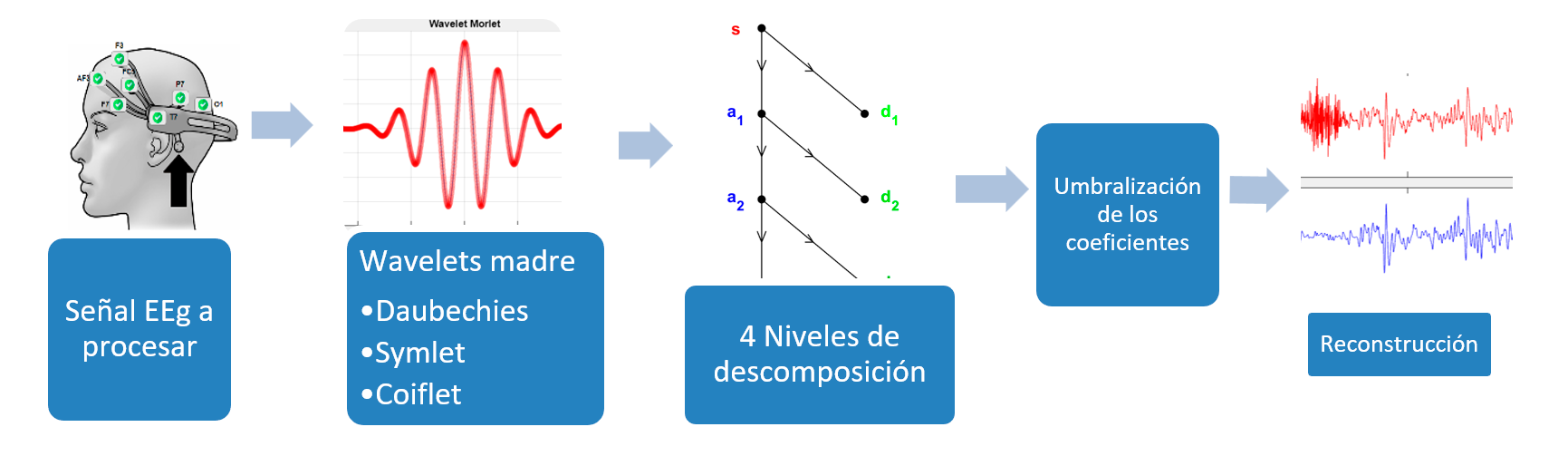
Figura 4. Diagrama a bloques de la metodología para el filtrado de una señal sintética contaminada con un artefacto muscular
En la figura 5 se muestra el filtrado de la señal aplicando la wavelet Daubechies 2 (db2); en la figura 5.a se presenta la señal original contaminada con un artefacto muscular y en la figura 5.b se presenta la señal filtrada con db2.
Para la evaluación del resultado, se aplicó el coeficiente de correlación de Pearson (r), el cual mide la relación lineal entre dos conjuntos de datos, obteniendo r=0.9318. A modo de comparación, se realiza el filtrado utilizando ICA y EMD obteniéndose r=0.7612.
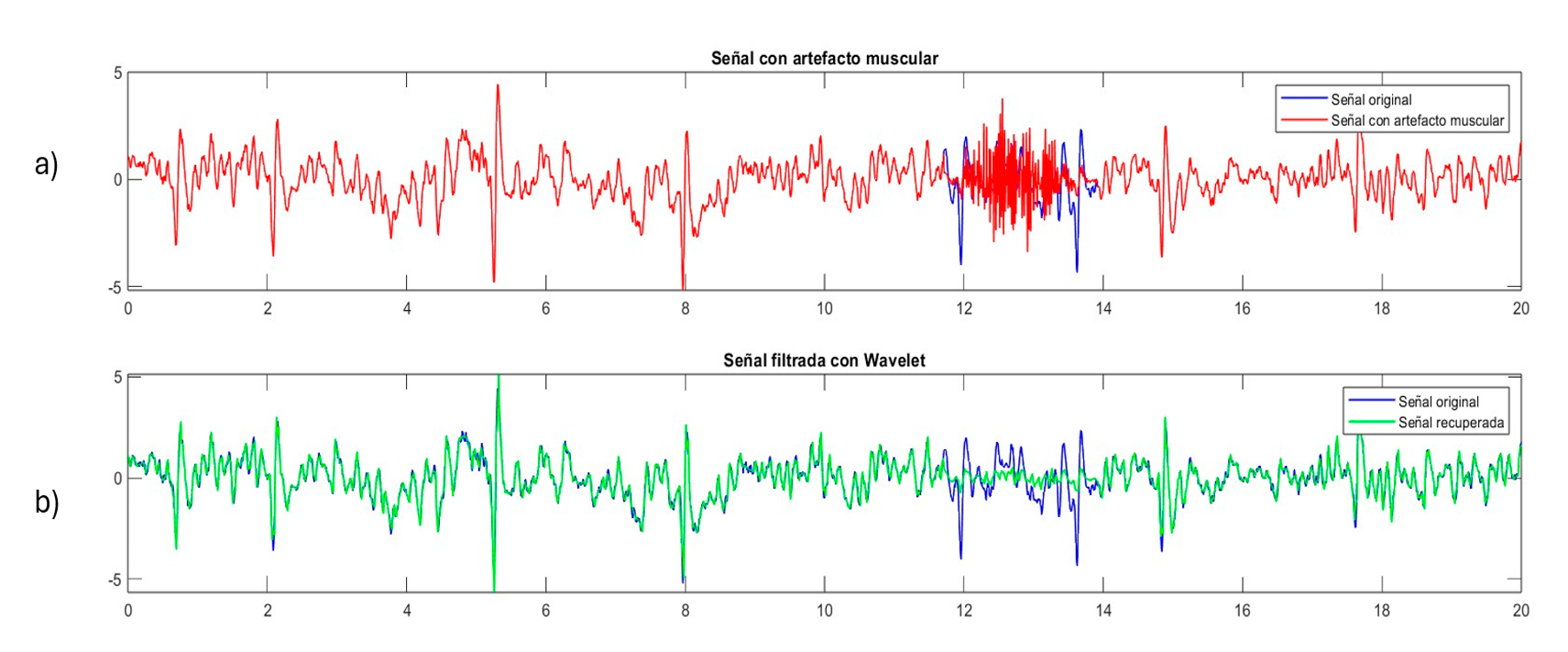
Figura 5. Filtrado de artefacto muscular en señal sintética de EEG con wavelet db2: a) Señal original de color azul y señal contaminada con artefacto muscular de color rojo, b) Señal resultante al aplicar filtro con db2 de color verde y señal original de color azul
Tabla
| Wavelet | Nivel desc. | r | Wavelet | Nivel desc. | r | Wavelet | Nivel desc. | r |
|---|---|---|---|---|---|---|---|---|
| Sym2 | 1 | 0.93761 | Coif2 | 1 | 0.93116 | Db3 | 1 | 0.93966 |
| 2 | 0.93178 | 2 | 0.94056 | 2 | 0.93810 | |||
| 3 | 0.86664 | 3 | 0.85008 | 3 | 0.86568 | |||
| 4 | 0.67327 | 4 | 0.69880 | 4 | 0.67520 | |||
| Sym3 | 1 | 0.93966 | Coif3 | 1 | 0.93256 | Db4 | 1 | 0.93697 |
| 2 | 0.93810 | 2 | 0.94267 | 2 | 0.94065 | |||
| 3 | 0.86568 | 3 | 0.88297 | 3 | 0.85688 | |||
| 4 | 0.67520 | 4 | 0.69907 | 4 | 0.70509 | |||
| Sym4 | 1 | 0.93121 | Coif4 | 1 | 0.93348 | Db5 | 1 | 0.93366 |
| 2 | 0.94002 | 2 | 0.94345 | 2 | 0.94251 | |||
| 3 | 0.87360 | 3 | 0.85813 | 3 | 0.87723 | |||
| 4 | 0.68250 | 4 | 0.67253 | 4 | 0.66504 | |||
| Sym5 | 1 | 0.93622 | Db1 | 1 | 0.92259 | |||
| 2 | 0.94215 | 2 | 0.90961 | |||||
| 3 | 0.87792 | 3 | 0.81832 | |||||
| 4 | 0.66798 | 4 | 0.68767 | |||||
| Coif1 | 1 | 0.92757 | Db2 | 1 | 0.93761 | |||
| 2 | 0.93082 | 2 | 0.93178 | |||||
| 3 | 0.86558 | 3 | 0.84664 | |||||
| 4 | 0.66685 | 4 | 0.67327 |
El módulo wavelet implementado en la interfaz promete convertirse en una herramienta útil y de fácil manejo para el análisis de señales electroencefalográficas. A manera de ilustrar su potencial se analizó una señal sintética contaminada con un artefacto muscular. Después del análisis se encontró que la wavelet Coiflet 4 presentó mejores resultados en función del coeficiente de correlación de Pearson.
Como se puede ver, la elección de una wavelet madre adecuada es esencial para garantizar que el proceso de filtrado sea efectivo, eficiente y produzca resultados precisos que capturen la información relevante en la señal original y poder realizar un correcto filtrado de la señal.
Aunque el filtrado del artefacto muscular en la señal sintética parece desaparecer por completo, el filtrado con wavelets respeta el rango en el que no se encuentra dicho artefacto a comparación del filtrado realizado con ICA y EMD que mantiene una tendencia similar a la señal original en el rango del artefacto, esto da paso a una posible combinación entre técnicas de filtrado. Como trabajo futuro se propone continuar el desarrollo del módulo e implementar las wavelets Meyer, Morlet, Daubechies, Biortogonal y Symlet.
Obtener PDF